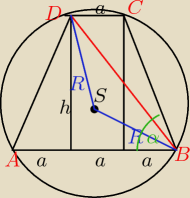
PROblem TOmek: Podstawą ostrosłupa jest trapez równoramienny o podstawach a,3a i kącie ostrym α. Krawędzie boczne są nachylone do podstawy pod tym samym kątem α. Oblicz objętość ostrosłupa. −−−−−−−−−−−−−−−−− obliczyłem prawidłowo Pole podstawy: h=a*tgα P=2a²tgα −−−−−−−−−− teraz trudniejszy moment gdzie mam problem. "Krawędzie boczne są nachylone do podstawy pod tym samym kątem α" czyli spodek wysokości to środek okręgu opisanego na podstawie − to jest pewne. I jak obliczyć ten promien. Obliczyłem przekątnej podstawy(prawidłowo):

	1
|BD|=a√		+3 koniec pierw.
	cos2α

lecz jak obliczyć ten nasz promien Męcze sie już 2h ...

TOmek:

TOmek: pomozice, prosze ICSP

TOmek: up

TOmek: prosze : (

b.: przychodzi mi do głowy tylko taka dość toporna metoda: 1. obliczamy odległość S od dłuższej podstawy (z tw. Pitagorasa) −− wychodzi, jeśli się nie pomyliłem, √R² − 9a²/4 2. obliczamy odległość S od krótszej podstawy −− chyba będzie √R²−a²/4 3. suma tych dwóch odległości musi dać h, czyli √R² − 9a²/4 + √R²−a²/4 = h = a tgα podnieśmy obustronnie do kwadratu: 2R² − 10a²/4 + 2√R² − 9a²/4 √R²−a²/4 = a² tgα teraz jak przeniesiemy 2R² − 10a²/4 na prawą stronę i znowu do kwadratu, to dostaniemy proste równanie kwadratowe na R² (skróci się 4R⁴, zostaną tylko R² i wyraz wolny). wiem, strasznie syfiaste, ale powinno doprowadzić do wyniku...

b.: pomyłka: powinno być a² tg²α po prawej stronie na końcu

TOmek: no troche jest tych obliczeń, myśle ,ze jest łatwiejszy sposob tylko za cholere nie mogę na niego wpaść. Dziekuje pięknie za pomoc

b.: aha, już widzę łatwiejszy sposób: ten okrąg jest też opisany na trójkącie ABD, skąd

	|BD|
R=
	2sin α

TOmek: no przecież to jasne ,dzieki pięknie

TOmek: czyli

	1   a√ +3   cos2
ctgα=
	H

tak?

TOmek: dzieki slicznie, zaraz dodam jedno zadanie rozwiązane bo nie wiem gdzie mam błąd

b.: chyba nie,

	R
ctg α =		,
	H

a R trzeba jeszcze wyliczyć

TOmek: źle zapisałem miało być:

	a√1/cos2+3   2sin
ctgα=		o tak ?
	H

b.: tak (oczywiście powinny być α w odp. miejscach...)