Basia: masz cztery możliwości:
1.
x≥m i x≥7
x−m+x−7 = 3
2x = m+10
| | m+10 | |
x = |
| nie ma nieskończenie wielu rozwiązań |
| | 2 | |
2.
x≥m i x<7
x−m + [−(x+7)] = 3
x−m −x − 7 = 3
−m = 10
m = −10
czyli masz
|x+10| + |x−7| = 3
i musi być x≥−10 i x<7
czyli jest nieskończenie wiele rozwiązań ∊ <−10;7)
3.
x<m i x≥7
−(x−m)+x−7 = 3
−x+m+x−7 = 3
m=10
i musi być x<10 i x≥7
czyli jest nieskończenie wiele rozwiązań ∊ <7, 10)
4.
x<m i x<7
−(x−m) + [−(x−7)] = 3
−x+m−x+7 = 3
−2x = −m − 4
| | m+4 | |
x = |
| nie ma nieskończenie wielu rozwiązań |
| | 2 | |
UWAGA:
w przypadkach (1) i (4) może być albo dokładnie jedno rozwiązanie, albo równanie będzie
sprzeczne, ale to już nie należy do rozwiązania, bo o to nie pytają
Eta:
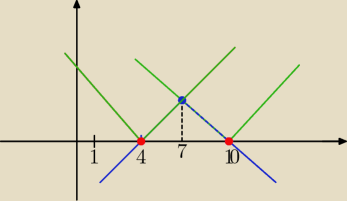
Można też graficznie
|x−m|= −|x−7| +3
f(x) = − |x−7| +3 i
g(x) = |x−m|
dla m= 4 lub m= 10 wykresy częściowo pokrywają się ( nieskończenie wiele rozwiązań)
