funkcja kwadratowa Krzysztofek: Napisz równanie stycznej do okręgu i prostopadłej do prostej k: o: x² +y² −2x +12y +28 =0 k: y=−1/2x

Basia: prosta prostopadła do k musi mieć równanie y = 2x + b ma być styczna do okręgu czyli układ równań (z parametrem b) x² + y² − 2x +12y +28 = 0 y = 2x+b musi mieć jedno i tylko jedno rozwiązanie (czyli Δ=0)

Trivial: Inny sposób. Oznaczmy prostą styczną przez s. s: y = 2x + b (z oczywistych powodów) Inaczej: 2x − y + b = 0 Musi być ona odległa od środka okręgu S dokładnie o R. Zatem... x² + y² − 2x + 12y + 28 = 0 (x−1)²−1 + (y+6)²−36 + 28 = 0 (x−1)² + (y+6)² = 9. S = (1, −6) R = 3. Odległość punktu od prostej:

	|Ax0 + By0 + C|		|2*1 −1*(−6) + b|		|b+8|
d(S, s) =		=		=		= 3
	√A2+B2		√4+1		√5

b2+16b+64
	= 9
5

b²+16b+64 = 45 b²+16b+19 = 0 Δ = ... b = ...

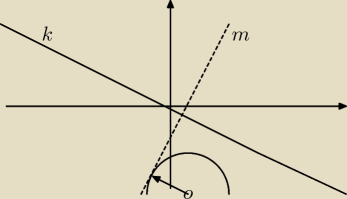
zibi: W celu sporządzenia rysunku przekształćmy równanie okręgu: x²+y²−2x+12y+28=0 ⇒ (x²−2x+1)−1+(y²+12y+36)−36+28=0 ⇒(x−1)²+(y+6)²−9=0 ⇒ (x−1)²+(y+6)²−9=0 ⇒ (x−1)²+(y+6)²=9 ⇒ (x−1)²+(y+6)²=3² ⇒ okrąg ma środek w punkcie (1;−6) i promień r=3. Z warunku prostopadłości szukanej prostej m do prostej k wynika, że prosta ta ma współczynnik kierunkowy wynoszący 2. Prosta m należy zatem do rodziny prostych określonych wzorem: y=2x+β. ciag dalszy nastapi bo zawiesiłem się

zibi: nic dodać nic ująć do rozwiązania Basi to się nazywa elegancja, moja propozycja zaś można porównać do przerzucania tony węgla łopatą

Trivial: zibi, twoja droga jest dobra i mniej rachunkowa niż metoda 'na deltę'.

Trivial: Jedyne co bym sugerował to: Wyrażenie: x² − 2px = (x−p)² − p². Czyli: x² − 2x = (x−1)²−1. y²+12y = (y+6)²−36. Szybciej.

Gustlik: Jest prostszy sposób przekształcenia równania okręgu, niz zwijanie wzorami skróconego mnożenia, są na to wzory: x² + y² + Ax + By + C = 0

	A
a=−
	2

	B
b=−
	2

r=√a²+b²−C, gdy a²+b²−C>0 Wzorami skrócopnego mnozenia jest zdecydowanie najdłuzej i najtrudniej. Wyprowadzenie wzorów tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1471 . x² + y² − 2x + 12y + 28 = 0

	A		−2
a=−		=−		=1
	2		2

	B		12
b=−		=−		=−6
	2		2

r=√1²+(−6)²−28=√1+36−28=√9=3 Mamy S=(1, −6), r=3, oraz (x−1)²+(y+6)²=9 C.D. metodą Triviala.