oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego
cysiek: oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego alfa wiedząc ze :
COS α= 3/4
SINα= pierwiastek 2 /2
ctg α= pierwiastek 5 /2
tg α = 1/2 (jedna druga)
ctg α= 3
2 paź 13:22
Eta:
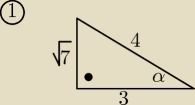
a
2= c
2−b
2 => a
2= 16−9=7 a=
√7
pozostałe podobnie .....

2 paź 13:33
cysiek: a dlaczego pierwiastek z 7 ?

2 paź 13:36
Eta:
bo
a >0 i a2= 7 => a= √7
2 paź 13:38
cysiek: rozumiem dziekii

pozdro
2 paź 13:40
Trivial: Metoda trójkąta jest genialna.

Nie wiem dlaczego nie spotkałem się z nią w szkole.
2 paź 13:41
cysiek:
przyznaje ja matematykiem nie jestem i bardzo slaby jestem i cwicze . pierwiastek z 2 razy
pierwiastek z 2 = ?
2 paź 13:44
Trivial: (√2)2 = ?
2 paź 13:45
cysiek: tak tak to ?
2 paź 13:45
Remik: 2
2 paź 23:33
Basia:
Trivial: Metoda trójkąta jest genialna.Nie wiem dlaczego nie spotkałem się z nią w szkole.
Bo jest poprawna jedynie dla kątów ostrych, a Ty byłeś na rozszerzeniu i musiałeś sobie radzić
z wszystkim kątami <0; 360) ( i dalej, ale to już z okresowości)
2 paź 23:37
Gustlik: Basiu, mozna rozwiazywać metodą trójkąta również dla katów >90 stopni, tylko przyjąć
ujemne długości przyprostokatnych, tam gdzie dana współrzędna jest ujemna. Tylko trzeba
narysować trójkąt w układzie współrzędnych. Wychodzi na 100 %, bo rozwiazywałem w ten sposób.
I też jest szybciej niż wzorami, w dodatku widać znaki funkcji w poszczególnych ćwiartkach.
2 paź 23:54
Basia:
nie wiedziałam, że odcinek może mieć ujemną długość
definicję funkcji trygonometrycznej kąta rozszerzonego wykorzystujesz, a nie żadną ujemną
długość, bo takie zwierzę nie istnieje (przynajmniej w geometrii euklidesowej)
3 paź 00:16
Gustlik: Napisałem "przyjąć ujemne dlugości przyprostokątnych, tam gdzie współrzędne są ujemne", co nie
oznacza, że są one ujemne. Czyli zaznaczyć np. −5 na przyprostokątnej trójkąta, tam gdzie dana
współrzędna jest ujemna i wynosi −5.
Basiu, ja naprawde znam definicje funkcji trygonometrycznych, naprawdę wiem, że nie
istnieje ujemna dlugość, tylko chodzi mi o obrazowe wytłumaczenie tej metody. Nie łap mnie za
słówka.
Ja lubię metody obrazowe, dlatego że są one łatwo przyswajalne dla uczniów, a przede wszystkim
pozwalają na szybkie sprawdzenie, czy zadanie zostało rozwiązane poprawnie.
Pozdrawiam

3 paź 00:24
Gustlik: Jeszcze jedno: spotkałem się w praktycznych obliczeniach, np. w fizyce, że w pewnych sytuacjach
przyjmuje się UMOWNIE długość za ujemną, co ułatwia rozwiązanie zadania. Np. w takich: pewna
osoba znajduje się w chwili początkowej w odległości 2 m od obserwatora z jego lewej strony,
po czym rusza w stronę obserwatora, mija go i zatrzymuje się w odległości 3 m z prawej strony.
I wtedy można przyjąć: położenie początkowe −2 m, położenie końcowe +3 m, a obserwator stoi w
punkcie 0. Zatem ta osoba przeszła 5 m, a znając np. czas przebycia tej drogi, obliczyc jej
prędkość. Oczywiście − są to współrzędne, wyprzedzam to, co mi zaraz powiesz, ale uczeń lepiej
zrozum ie: z lewej strony "ujemna" odległość, a z prawej strony − "dodatnia". Dlatego
napisałem − PRZYJMUJEMY.
Pozdrawiam.
3 paź 00:31
Basia:
przyzwoite tłumaczenie tej metody polega na pokazaniu, że np. w II ćwiartce
|OP| = r |PPx| = y natomiast |PPy| = |x| = −x
z czego zresztą natychmiast wynikają wzory redukcyjne
3 paź 00:32
Basia:
odległość od A do B = |AB| i nie może być ujemna
to nie jest nauka
3 paź 00:34
Gustlik: Zgadza się i ja to tak pokazuję i rozrysowuję. Tylko zaznaczam wartość współrzędnej, również
ujemną, na przeciwprostokątnej trójkąta, tak, jakby była to długość, bo wtedy widać, co się
skąd bierze. Dlatego tak to określiłem. Powtarzam − napisałem "PRZYJMUJEMY", czyli pewna
umowa.
3 paź 00:36
Gustlik: Basia, ja to wszystko wiem, ale trzeba założyć: obserwator stoi w punkcie 0, a dla tych, co
stoją z lewej strony − przyjmujemy ujemne położenie, czyli ujemne współrzędne, natomiast dta
tych, co stoją z prawej strony − dodatnie współrzędne. Droga
Basiu, naprawdę nie musisz
mnie uczyć takich podstawowych rzeczy. Ja już Ci powiedziałem, że to jest współrzędna, dlatego
jest ujemna, ale nanoszę ja jak długość, bo wtedy widać. I tak to tłumaczę uczniom.
Pozdrawiam serdecznie

3 paź 00:39
pina: sinα=0,7
17 wrz 17:50
Marta : Zad.1. Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego alfa.
a) tg alfa=50
b) tg alfa pierwiastek z 2
Zad.2 Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego alfa.
a) cos alfa= dwie piąte
b) cos alfa= pierwiastek z trzech kredka ułamkowa a na dolę dwa.
6 gru 15:13
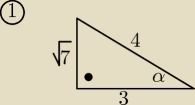 a2= c2−b2 => a2= 16−9=7 a= √7
a2= c2−b2 => a2= 16−9=7 a= √7


 pozdro
pozdro
 Nie wiem dlaczego nie spotkałem się z nią w szkole.
Nie wiem dlaczego nie spotkałem się z nią w szkole.

