2 paź 10:47
Godzio:
Nie ma
2 paź 10:49
BethP: No to dupa. A może wiesz jak to rozwiązać?
2 paź 10:50
Godzio:
Daj mi chwilę
2 paź 10:53
Problemowa: W tym zadaniu trójkąt BOC jest równoboczny. Więc kąt BOC ma miarę 600. Skoro prosta k jest
styczną okręgu to kąt ACO jest równy 900. Więc o ile się nie mylę kąt α wynosi 300
2 paź 10:54
BethP: No dobra. Właściwie to chyba nie mam innego wyjścia
2 paź 10:54
BethP: Tak, Problemowa masz rację. Dzięki
2 paź 10:56
Godzio:
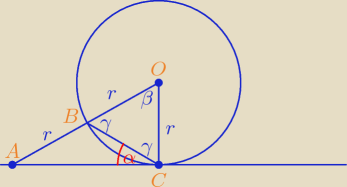
| | r | | 1 | | 180 − 60 | |
cosβ = |
| ⇒ sinβ = |
| ⇒ β = 60o ⇒ γ = |
| = 60o |
| | 2r | | 2 | | 2 | |
α + γ = 90
o ⇒ α = 30
o
2 paź 10:56
Problemowa:
2 paź 10:56
BethP: Dzięki wielkie. A móglibyście mi jeszcze pomóc z tym czymś?
1. Punkty A, B, C są kolejnymi wierzchołkami równoległoboku ABCD. Oblicz współrzędne
wierzchołka D i obwód równoległoboku, gdy A(−2, 3), (7,2), (0,5)
2. Punkty A,B,C takie że A(0,0) B(3,1) C(4,3) są kolejnymi wierchołkami równoległoboku ABCD.
a) Oblicz obwód równoległoboku
b) Oblicz odległość punktu C od prostej AB
c) Oblicz pole równoległoboku.
2 paź 10:59
Problemowa: 1. Ja bym policzyła z różnicy współrzędnych punktu. Jeżeli oznaczymy równoległobok tak jak we
wzorach maturalnych to długość boku a = (−2)−7 = 9 jednostek a wysokość h = 5−2 = 3 jednostki.
więc współrzędne punktu D to by było x=0−9=−9 a y = 3+3 = 6. więc mamy (−9,6) ale nie wiem czy
to na pewno dobrze
2 paź 11:03
Godzio:
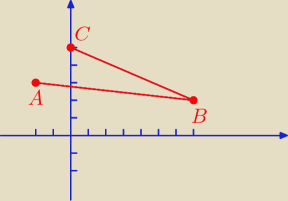
1. Np. tak: Wyznacz środek AC (będzie to automatycznie środek BD) policz prostą przechodzącą
przez B i S
AC, i wiedząc że |AB| = |DC| zrób układ równań i go rozwiąż jak nie dasz rady to
daj znać
2 paź 11:05
Godzio:
Problemowa nie wiem czy takie coś było by uznane
2 paź 11:05
Problemowa: Ale zdecydowanie prostsze
2 paź 11:06
Godzio:
Wiadomo
2 paź 11:08
Problemowa: Drugie zdanie jest podobne do 1., więc raczej większych problemów nie powinieneś mieć
2 paź 11:08
BethP: Godzio, nie dam rady.
2 paź 11:09
Godzio:
2. Tylko i wyłącznie działasz na wzorach, napisz sobie wzór na długość odcinka
a) L = 2 * (|AB| + |BC|)
b) odległość punktu od prostej
c) P = dodl. punktu C od AB * |AB|
2 paź 11:09
Godzio:
A próbowałeś ? Za 10 min wracam i chce zobaczyć początek chociaż, wyznacz środek i wyznacz
prostą przechodzącą przez ten środek i punkt B, dalsza część jest trudniejsza, ale to musisz
umieć zrobić
2 paź 11:10
Problemowa: | | xA+xC | | yA+yC | |
Środek możesz wyznaczyć ze wzoru, czyli SAC=( |
| , |
| ) Więc wyjdzie |
| | 2 | | 2 | |
(−1,4)
2 paź 11:15
Problemowa: Dalej równanie prostej możesz wyznaczyć z dwóch punktów, które należa do tej prostej czyli
SAC=(−1,4) i B=(7,2). Podstawiasz x i y do wzoru ogólnego prostej czyli y = ax+b i masz
układ równań: 2 =7a+b i 4=−a+b
2 paź 11:18
Problemowa: | | 1 | | 3 | | 1 | | 3 | |
Stąd wiesz, że a = − |
| a b=3 |
| Więc równanie prostej będzie y =− |
| x+3 |
| |
| | 4 | | 4 | | 4 | | 4 | |
2 paź 11:22
Godzio:
Łohoho
To widzę, że
BethP się natrudził/a
2 paź 11:25
BethP: Trochę inaczej to wszystko policzyłam, ale wyszło mi tak, że D(−9,6),
a L=2({82}+{58}). Chyba dobrze, bo nie mam odpowiedzi do tej książki
2 paź 11:25
Godzio:
Jest ok
2 paź 11:27
BethP: te nawiasy {} to miały być pierwiastki
2 paź 11:27
Godzio: Domyśliłem się p { } = √
2 paź 11:29
Problemowa: Moja pomoc okazała się zbyteczna
2 paź 11:29
BethP: W każdym razie dzięki wielkie za pomoc. Godzio żadna 'dupa' po prostu jestem humanistką, nie
umysłem ścisłym dlatego nie robię tych zadań tak szybko jak wy
2 paź 11:30
Godzio:
Nie chodzi, ze nie robisz tak szybko, tylko po co zakładasz nowy wątek skoro masz tu wszystko
napisane, wzory chyba masz
2 paź 11:30
BethP: Każda pomoc jest potrzebna, gdy jest się tępym jak ja
2 paź 11:31
Problemowa: Spokojnie, zadanie rozwiązane i to najważniejsze
2 paź 11:31
Jack:
obrażasz humanistów
Jesteś co najwyżej leniem a nie humanistką...
2 paź 11:31
Problemowa: Widzę, Godzio, że też się nie nudzisz tylko od rana na forum, służysz bezinteresowną pomocą
2 paź 11:32
BethP: No bo wstawiłam to akurat w tym momencie, w którym mi odpowiedziała Problemowa (raczej
bezproblemowa
2 paź 11:32
Godzio:
A co można robić w niedzielę rano, po za tym czekam aż przyjdzie do mnie typek na korki
, a
pomocą służę już dokładnie 2 lata, dokładnie w październiku w 2009 roku tu wpadłem i zostałem
2 paź 11:33
BethP: Jack, wiem co mówię u mnie ma tak cała klasa. A leniem raczej nie jestem, bo gdybym była to
jutro wzięłabym po prostu kropkę.
2 paź 11:34
Jack:
ja też znam wielu humanistów, chyba żaden z nich nie broni się w ten sposób. Rozumiem że możesz
nie mieć wiedzy, ale myśleć potrafią
nawet humaniści
Piszę to po to, żeby uzmysłowić Ci że humanista tez potrafi skutecznie działać na polu
matematyki
2 paź 11:37
Problemowa: Czego sam jesteś dobrym przykładem
2 paź 11:39
Jack:
z grzeczności nie zaprzeczę
2 paź 11:49