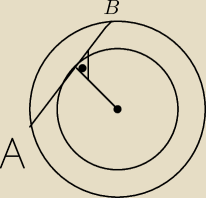
Geometria Pomocy :): Na rysunku obok przedstawione są dwa okręgi o wspólnym środku O i różnych promieniach. Punkty A i B należą do dużego okręgu, zaś odcinek AB długości 12cm jest styczny do małego okręgu. Oblicz pole pierścienia kołowego ograniczonego tymi okręgami.

ja: Pole pierscienia 36 π Oznacz sobie r−promien malego kola R promien duzego i skorzystaj z Twierdzenia Pitagorasa

ja: Korzystajac z rysunku http://zapodaj.net/2eec7891423c.jpg.html Masz policzyć P=πR²−πr²=π(R²−r²) Ale w trójkącie ABC z Tw. Pitagorasa mamy R²=r²+6²⇒ R²−r²=36 co podstawiamy do powyższej równości i mamy wynik 36π

wioletta: na rysunku są dwa odcinki będące promieniami tego samego okręgu .narysuj ten okrą na