 Będę bardzo wdzięczna.
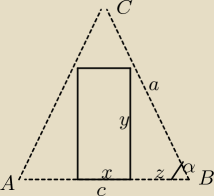
W trójkąt równoramienny ABC, w którym | AB | = c, | BC | = | CA | = a wpisujemy prostokąty tak,
że jeden bok prostokąta zawiera się w boku AB, a dwa pozostałe wierzchołki należą do ramion
trójkąta. Podaj wymiary prostokąta o największym polu.
Będę bardzo wdzięczna.
W trójkąt równoramienny ABC, w którym | AB | = c, | BC | = | CA | = a wpisujemy prostokąty tak,
że jeden bok prostokąta zawiera się w boku AB, a dwa pozostałe wierzchołki należą do ramion
trójkąta. Podaj wymiary prostokąta o największym polu.
 x−dlugosc boku bedacy prostopadly do podstawy trojkata
y−rownolegly do podstawy trojkata
h=√a2=0,25c2
P=xy
x−dlugosc boku bedacy prostopadly do podstawy trojkata
y−rownolegly do podstawy trojkata
h=√a2=0,25c2
P=xy
| h−x | 2h | ||
= | |||
| y | c |
| c(h−x) | ||
y= | ||
| 2h |
| cx(h−x) | c | c | ||||
P=x*y= | =− | x2+ | x | |||
| 2h | 2h | 2 |

 Pole prostokąta:
P=x*y
bok x=c−2*z
bok y=z*tgα , wstawiamy do wzoru na pole P:
P=(c−2*z)*z*tgα , zauważ, że jedyną zmienną jest "z", bo c i tgα to stałe.
przekształcamy powyższy wzór:
P=z*c*tgα − z2*2*tgα, jest to funkcja kwadratowa ze zmienną "z". Z uwagi na ujemną wartość
parametru przy z2 parabola będącą wykresem ma ramiona skierowane w dół, czyli jej wartość
ekstremalna jest maksimum. Aby znaleźć ekstremum funkcji należy jej pochodną porównać do zera,
i znaleźć rozwiązanie takiego równania:
pochodna P'=c*tgα − z*4*tgα, porównujemy do zero: c*tgα − z*4*tgα = 0 ⇒ c*tgα = z*4*tgα
⇒z = c*tgα / 4*tgα ⇒ z = c/4
Pole prostokąta:
P=x*y
bok x=c−2*z
bok y=z*tgα , wstawiamy do wzoru na pole P:
P=(c−2*z)*z*tgα , zauważ, że jedyną zmienną jest "z", bo c i tgα to stałe.
przekształcamy powyższy wzór:
P=z*c*tgα − z2*2*tgα, jest to funkcja kwadratowa ze zmienną "z". Z uwagi na ujemną wartość
parametru przy z2 parabola będącą wykresem ma ramiona skierowane w dół, czyli jej wartość
ekstremalna jest maksimum. Aby znaleźć ekstremum funkcji należy jej pochodną porównać do zera,
i znaleźć rozwiązanie takiego równania:
pochodna P'=c*tgα − z*4*tgα, porównujemy do zero: c*tgα − z*4*tgα = 0 ⇒ c*tgα = z*4*tgα
⇒z = c*tgα / 4*tgα ⇒ z = c/4
