Elementy stytystyki opisowej.Teoria prawdopodobieństwa i kombinatoryka Tancerz: Zadanie dla Godzia Słyszłem od innych forumowiczów że jesteś dobry z matmy W pudełku znajduje się 10 kul białych i 8 kul czarnych. Losujemy trzy kule. Sporządź drzewo tego doświadczenia losowego i oblicz prawdopodobieństwo: a) zdarzenia A, że wylosowano dwie kule czarne, b) zdarzenia B, że wylosowano co najmniej dwie kule czarne, C) zdarzenia C, że wylosowano co najmniej jedną kulę czarną nie brałem tego jeszcze wogóle w szkole proszę cie o wytłumaczenie

tancerka: a gdzie słyszałeś?

Tancerz: od znajomych którzy korzystają z tego forum

Tancerz: Godzio mam problem bo nie wiem jak to policzyć jakbyś mi pomógł w zadaniu, chciałbym to zrozumieć, wiem że do takich jak ja trzeba ciepliwości

Godzio: Moment Mam już doświadczenie z "trudnymi przypadkami" także spokojnie, damy radę

Tancerz: ja tego zadanie nie mogę ruszyć proszę cię o wytłumaczenie i rozwiązanie

Eta: pamiętaj Godzio o "krzakach"

Godzio:

n 1		n n
	= n,		= 1

	18 3		18!
Ω =		−− losujemy 3 kule z 18 to jest chyba oczywiste ... =		=
			3! * 15!

	15! * 16 * 17 * 18
=		= 816
	1 * 2 * 3 * 15!

	8 2	10 1
a) A =			−− losujemy 2 kule czarne i jedną białą (z tych co mamy dostępne)

	8!		6! * 7 * 8
... =		=		= 28
	2! * 6!		1 * 2 * 6!

	A
P(A) =		= ...
	Ω

b) [co najmniej 2 kule → albo wyciągniemy 2 kule czarne (i jedną białą) albo 3 (i 0 białych) ]

	8 2	10 1		8 3	10 0		8!
B =			+			= 28 +		* 1 =
							3! * 5!

	5! * 6 * 7 * 8
28 +		= 28 + 56 = 84
	1 * 2 * 3 *5!

	B
P(B) =		= ...
	Ω

c) Spróbuj sam, co najmniej jedna kula czarna oznacza: albo jedną kulę czarną i dwie białe lub dwie kule czarne i jedną białą lub trzy kule czarne i 0 białych, (patrz. b) ) W razie co pytaj, drzewka trzeba narysować do każdego zdarzenia ?

Tancerz: postaram się to zadanie zrozumieć czekam na pomoc

Godzio: Wyśle skan krzaków, bo tutaj za szybko ich nie narysuje

Tancerz: a drzewka narysujesz mi

Gustlik: Takich zadan NIE ROBI SIĘ DRZEWAMI ! Krzakoterapia w tym przypadku to sposób "dookoła świata". Od tego jest kombinatoryka. Symbol silni: n!=1*2*3*4*...*n − iloczyn kolejnych liczb od 1 do n. Przyjmuje się, że 0!=1 i 1!=1.

	18 3		18!		15!*16*17*18
|Ω|=C183=		=		{15!}=		=816 (wyciągasz w liczniku
			3!		15!*1*2*3

"wiekszą silnię" z mianownika, w tym przypadku 15!, domnażasz do końca, czyli do 18, w mianowniku rozpisujesz 3!, po rozipsaniu skracasz 15! oraz pozostałe czynniki licznika i mianownika, które można).

	8!		10!		6!*7*8		9!*10
|A|=C82*C101=		{6!}*		{9!}=		*		=28*10=280
	2!		1!		6!*1*2		9!*1

(muszą być dwie kombinacje, bo skoro mamy wylosować 2 kule czarne z 8, a losujemy 3 kule, to trzeba "dolosować" 1 kulę białą z 10, zawsze gdy losuje się elementy dwóch rodzajów, to mnoży się kombinacje jednych przez kombinacje drugich − zwykła reguła mnożenia).

	280
P(A)=		≈0,343
	816

c.d.n. zaraz wrócę, zrobię resztę.

sushi_ gg6397228: Losujemy trzy kule. −−> nic nie pisze czy od razu wszystkie (drzewko niepotrzebne) czy pojedynczo ze zwracaniem czy bez zwracania

Tancerz: nic nie pisze że bez z wracania czy z wracanie

sushi_ gg6397228: ani czy 3 na raz czy pojedynczo−−> a to ma znaczenie, bo wtedy sie liczy to dla TRZECH róznych wzorów

Tancerz: nic sprawdzałem

Godzio: W a) zjadłem 10, 280 oczywiście powinno być

Tancerz: a narysujesz mi drzewko Godzio

Tancerz: nie wiem jak tu się rysuje drzewa

Godzio: Coś mi to drzewko wyjść zgodnie z odp. nie chce

Gustlik: Widzę, że Godzio zrobił zadanie jak trzeba, chciałem zrobić tym samym sposobem. Pozdrawiam

Problemowa: w b) też powinno być 280+56=336

Problemowa: w b) też powinno być 280+56=336

Godzio: No bo przepisywałem od razu z A to stąd ten błąd

Problemowa: Ale patrz, w tym zadaniu drzewko i tak jest bez sensu totalnie. To nie łatwiej by było założyć, że kulki są identyczne i za pierwszym razem są 2 sposoby wylosowania kulki (Biała lub Czarna), za drugi razem już będą 4 kombinacje kolorów no i na koniec 8... ?

Gustlik: C) zdarzenia C, że wylosowano co najmniej jedną kulę czarną To można zrobić z dopełnienia − wtedy rozpatrujemy jeden przypadek zamiast trzech: C' − nie wylosowano kuli czarnej (czyli same białe)

	10 3		10!		7!*8*9*10
|C'|=C103=		=		{7!}=		=120
			3!		7!*1*2*3

|C|=|Ω|−|C'|=816−120=696

	696
P(C)=		≈0,85
	816

Godzio: Też tak chciałem zrobić, ale stwierdziłem że skoro mamy już podpunkt b to zadanie jest tak samo proste robiąc metodą z dopełnieniem

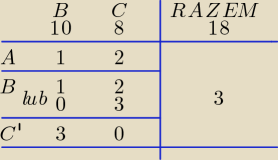
Bogdan: Proponuję takie rozwiązanie:

	10 1   8 2   *		8*7   10 *   1*2
P(A) =		=		=
	18 3		18*17*16     1*2*3

...

	10 1   8 2   10 0   8 3   * + *
P(B) =		= ...
	18 3

	10 3   8 0   *
P(C) = 1 − P(C') = 1 −		= ...
	18 3

Tancerz: gdzie w podpunkcie a) zjadłeś 10 możesz napisać

Problemowa:

	8 2	10 1		8!
Godzio pominął w wyniku drugi symbol Newtona. Powinno być A=			=		*
				2!6!

	10!
		= (tak jak Godzio obliczył) 28 * 10 (z drugiego symbolu Newtona) = 280
	1!9!

Tancerz: Godzio rozpisz mi proszę w który miejscu w podpunkcie a) ma być 10

Problemowa: No przecież Ci już rozpisałam

Tancerz: Godzio narysuj mi drzewka albo wrzuć zdjęcie to ważne

Godzio: Problemowa to rozpisała ale ok

	8 2		10 1		8 2
A =		*		= 28 * 10 = 280		masz wyliczone na początku, dochodzi

	10 1		n 1
tylko		= 10 (na początku napisałem		= n )