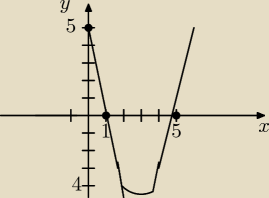
;) danonek: a)Podaj dla jakiego argumentu funkcja przyjmuje najmniejszą wartość; b)Oblicz wartość wyrażenia f(0)−4*f(−5) c)Podaj liczbę rozwiązań równania f(x)=−2

danonek: odpowiedzi to : a ) x=3 lub x=−3 b ) 5 c) 4 rozwiazania

danonek: wytłumaczy mi to ktoś?

danonek: nie ma chetnych?

Sławek: a) z rysunku wynika, że dla x=3 możemy też odczytać: x_w = 3, y_w= −4, f(0)=5, x₁=1, x₂=0 Zapiszemy równanie w postaci kanonicznej i obliczymy parametr 'a' f(x)=a(x−p)²+q f(x)=a(x−3)²−4 f(0)= a(0−3)²−4 5 = a(0−3)²−4 5 = 9a−4 9a = 5−4 9a=9 a=1 to samo równanie: − w postaci kanonicznej f(x)=(x−3)²−4 − w postaci iloczynowe f(x)=(x−1)(x−5) − w postaci ogólnej f(x)=x²−6x+5 pkt. b) f(0)=5 f(−5)=(−5)²−6*(−5)+5=25+30+5=50 f(0) − 4* f(−5) = 5 − 4*60 = 5 − 240 = −235 coś mi tu nie gra idę spać A tak w ogóle czy to dobry rysunek i treść oraz odpowiedzi?

danonek: wszystko jest tak jak w ksiażce

sushi_ gg6397228: zadanie trzeba zrobic z postaci iloczynowej y=a(x−x₁)(x−x₂) x₁=1 x₂=5 x=0 y=5 a=.... wyliczamy z czerwonego wzoru x_w=3 , potem mozna podstawic pod wzor czerwony i wyliczyc y=y_w