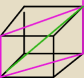
znam odpowiedz,ale nie rozumiem... zuzia: Prosze o zrobienie i wytlumaczenie... Przekątna prostopadłościanu ma dlugosc 2 i tworzy z krawędziemi prostopadloscianu,rowne kąty.Podaj wymiary tego prostopadłościanu.wychodzi na to ze to rozowe to kwadrat,,wiec jak to moze byc szescian?

Grześ: Tak, może to być sześcian... z przynależności "grup" brył jasno wynika, że sześciany zawierają się w prostopadłościanach

zuzia: tak,wiem,ale jesli czesc ktora zaznaczylam na rozowo to kwadrat,to nie mozliwe ze to szescian,bo wtedy przekatna podstawy i krawedz boczna sa rowne a wtedy to nie szescian. Ja bym prosila zeby mi to ktos od podstaw wyjasnij uwzgledniajac katy..

zuzia: ?

zuzia:

Problemowa: Skoro przekątna prostopadłościanu tworzy z krawędziami równe kąty to wiemy, że przekątna podstawy tego prostopadłościanu i jedna z jego krawędzi (załóżmy, że wysokość) ma długość 2=a√2 czyli a=√2. to te różowe linie na Twoim rysunku. Może to rozjaśni Ci sytuację

Jack: (widzę, że zaczynasz się wkręcać )

zuzia: Dalej nie za bardzo rozumiem i nie jestem pewna o co chodzi z tymi rownymi katami bo to mozna roznie odbierac...nie wiem:(

Problemowa: zielona przekątna prostopadłościanu, różowa krawędź i różowa przekątna podstawy tworzą trójkąt równoramienny

zuzia: chcesz powiedziec ze przekatna podstawy i rozowa krawedz maja taka sama dlugosc?

zuzia: ale wtedy to nie bedzie szescian a ma byc,tak jest w odpowiedzi

Problemowa: A no tak... To w takim razie trzeba to zrobić wyznaczając sinusy z trójkątów utworzonych przez przekątną i wtedy przyrównując je wyjdzie Ci, że jest to sześcian

zuzia: A mogłabyś mi to pokazać?

Problemowa: Skoro kąty, które tworzy przekątna z krawędziami są równe stąd mamy pewność, że sinusy tych kątów będą jednakowe

Problemowa: Czekaj

Problemowa: rozrysuj prostopadłościan i oznacz każdy wierzchołek ABCDEFGH i długości boków a−dł b−szer i c−wys to Ci pokaże o co chodzi

krystek: Złe założenia zrobiłyście .jeżeli oznaczysz sobie krawędzie tego prostopadłościanu a ,b ,c

	a		B		c
to z warunków zad masz		=sinα ,		=sinα i		=sinα
	d		d		d

stąd a=b=c

krystek: oczywiście cosα, pomyłka moja

Problemowa:

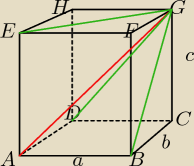
BG		EG		DG
	= sin ,		= sin ,		= sin . Przyrównujesz kolejno te wartości,
AG		AG		AG

	BG
podstawiając pod długości przekątnych, odpowiednie długości boków, czyli		=
	AG

	√a2+c2		EG		√a2+b2		DG		√a2+c2
		,		=		,		=		. No i teraz
	2		AG		2		AG		2

przyrównujesz pierwszą wartość do drugiej i wyjdzie Ci, że boki są równe, i kolejno tak samo robisz z drugą i trzecią parą.

Problemowa: Chyba Krystka sposób jest zdecydowanie prostszy

zuzia: Dziękuję