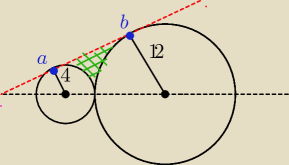
 ]Dwa okręgi styczne zewnętrznie mają promienie r=4 i R=12. Prosta AB jet wspólną styczną tych
okręgów. Oblicz pole zacieniowanego obszaru.
]Dwa okręgi styczne zewnętrznie mają promienie r=4 i R=12. Prosta AB jet wspólną styczną tych
okręgów. Oblicz pole zacieniowanego obszaru.
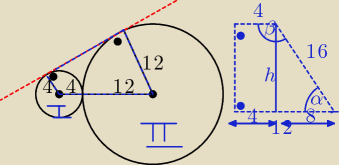 Policzmy pole tego trapezu, oraz interesują nas kąty α i β.
h2 + 82 = 162
h2 = 256 − 64
h2 = 192
h = 8√3
Policzmy pole tego trapezu, oraz interesują nas kąty α i β.
h2 + 82 = 162
h2 = 256 − 64
h2 = 192
h = 8√3
| 8 | 1 | |||
cosα = | = | ⇒ α = 60o zatem β = 120o | ||
| 16 | 2 |
| 12 + 4 | ||
Ptrapezu = | *8√3 = 64√3 | |
| 2 |
| 120 | 1 | 16 | 1 | |||||
PI = | *(πr2) = | *(π42) = | π = 5 | π | ||||
| 360 | 3 | 3 | 3 |
| 60 | 1 | |||
PII = | *(πR2} = | *(π122) = 24π | ||
| 360 | 6 |
| 1 | ||
Pwycinka = Ptrapezu − (PI + PII) = 64√3 − 29 | π | |
| 3 |