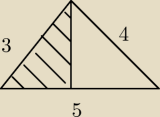
 oblicz pola zacieniowanych figur.
oblicz pola zacieniowanych figur.
| 1 | ||
Jego pole wynosi: | *3*4=6 | |
| 2 |
| 1 | ||
skoro pole jest równe 6 to | *5*h=6 | |
| 2 |
| 12 | ||
to h= | ||
| 5 |
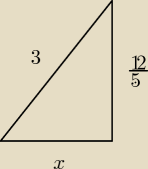 odszukaj z tw Pitagorasa bok x
i potem wylicz pole na pole Δ−a
odszukaj z tw Pitagorasa bok x
i potem wylicz pole na pole Δ−a

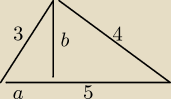 Trójkąt "duży" i trójkąt zacieniowany są trójkątami podobnymi. Oznaczmy przyprostokątne
trójkąta zacieniowanego jako "a" i "b".
Z podobieństwa trójkątów wynika, że: a:b = 3:4 stąd a = (3/4)b (1)
a także: b:3 = 4:5, stąd: b = 12/5 (2)
Wstawiając wynik (2) do (1) otrzymujemy:
a = (3/4) * (12/5) = 9/5
Pole zacieniowanego trójkąta wynosi: P = 0,5 * a *b . Podstawiając do wzoru wyliczone wcześniej
wartości a i b otrzymujemy:
P= 0,5 * (12/5) * (9/5) = 36/25 = (6/5)2
Trójkąt "duży" i trójkąt zacieniowany są trójkątami podobnymi. Oznaczmy przyprostokątne
trójkąta zacieniowanego jako "a" i "b".
Z podobieństwa trójkątów wynika, że: a:b = 3:4 stąd a = (3/4)b (1)
a także: b:3 = 4:5, stąd: b = 12/5 (2)
Wstawiając wynik (2) do (1) otrzymujemy:
a = (3/4) * (12/5) = 9/5
Pole zacieniowanego trójkąta wynosi: P = 0,5 * a *b . Podstawiając do wzoru wyliczone wcześniej
wartości a i b otrzymujemy:
P= 0,5 * (12/5) * (9/5) = 36/25 = (6/5)2
