rownanie Stokrotka: Rozwiąż metodą graficzną równanie: m(4^x−2^x)=1−m

	1
doszłam do postaci t2−t+1=
	m

narysowałam lewą stronę i nie wiem co dalej.. pomoże mi ktoś ?

Grześ: Jestem peny, że nie takie było polecenie do zadania. A określisz dokładnie co kryje się u Ciebie pod słowem "rozwiąż"

Sabin:

	1 − m
Zamiast twojej postaci proponuję t2 − t =		, gdzie m ≠ 0 oraz t > 0.
	m

Zauważ że skoro zmienną jest t, to dla ciebie funkcja po prawej stronie równania jest funkcją stałą − czyli poziomą linią prostą na wykresie. Sprawdź w ilu miejscach przetnie się taka linia prosta z wykresem twojej funkcji. To będą rozwiązania.

Stokrotka: rozwiąż czyli wyznacz ile rownanie ma to rozwiazan wzgledem parametru m . a mozesz mi to narysowaC? bo narysowałam, wyszla mi parabola, prowadze te proste ale nie wychodzi mi tak jak w odpowiedziach

Trivial:

	1
t2−t+1 =
	m

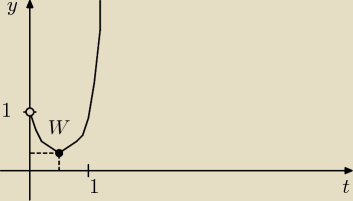
Ja tam wolę pierwszą postać: y(t) = t²−t+1 Rysujemy:

	1
p =
	2

	3
q =
	4

t>0 Dla t=0 mamy y(t) = 1. Czyli:

	1
0 rozw dla		< q
	m

	1		1
1 rozw dla		= q lub		≥ 1
	m		m

	1
2 rozw dla		∊(q, 1)
	m

I teraz wyznaczyć m.

Sabin: O, już masz wyjaśnienie, nawet w swojej wersji zapisu.

Skipper: Nie wiem czy tak można ...wszak pierwotna funkcja parabolą nie jest ... Moim zdaniem należy rozpatrywać funkcję y=4^x−2^x. Wykresem tej funkcji nie jest parabola.

Sabin: To już wiesz, że można...

Trivial: Jeszcze trzeba dodać potem, że dla m = 0 mamy 0 rozw.

Skipper: Moim zdaniem należy narysować wykres y=4^x ... odjąć od niego wykres y=2^x ... a potem "nałożyć"

	1
na to wykres y=		−1
	m

Skipper: No widzisz Sabin .... wiem, że nie można !

Trivial: Ale odwzorowanie t: R∍x → 2^x=t ∊ (0, +∞) jest bijekcją, więc śmiało możemy robić tą metodą.

Skipper: ... tak samo trywialne jak dla m=0

Stokrotka: i tak nie wychodzi

Sabin: Drogi Skipperze: skoro twierdzisz, że nie można, to uzasadnij To jest absolutnie poprawny sposób. I już widzę, jak graficznie za pomocą kartki papieru i ołówka odejmujesz funkcję 2^x od 4^x...

Sabin: Ach, zapomniałem. Co ci nie wychodzi Stokrotko? Postaraj się i napisz swoje rozwiązanie, byśmy mogli pomóc ci znaleźć błąd.

Trivial:

	1		3
0 rozw. dla		<		lub m = 0
	m		4

	3
m <		m2
	4

	3		4
0 <		m(m−		)
	4		3

	4
m∊(−∞, 0]∪(		, +∞)
	3

	1		3		4		1
1 rozw. dla		=		⇔ m =		lub		≥ 1. Zauważamy, że m>0, zatem:
	m		4		3		m

m ≤ 1 i m > 0

	4
m ∊(0, 1]∪{		}
	3

	4
2 rozw. dla m ∊ (1,		)
	3

Stokrotka: Już wszystko wiem ! bardzo wam dziekuje za pomoc buziaki