pomocy!
banan!: Dany jest graniastosłup prawidłowy czworokątny, którego pole powierzchni bocznej jest równe 480
cm2, a pole całkowite − 530 cm2. Oblicz sinusa kąta, jaki tworzy przekrój ABC1D1 tego
graniastosłupa.
26 wrz 20:45
Stachu: rysunek przedstaw
26 wrz 20:47
banan!:
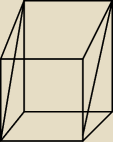
26 wrz 20:53
banan!: jak są te kreski po bokach to jest to wypełnione [nie umiem rysować tu]

26 wrz 20:53
Stachu: P
c= 530
P
c= 2P
p+P
b z tego możemy obliczyć pole podstawy ⇒
| | Pc−Pb | | 530−480 | |
Pp= |
| = |
| =25 |
| | 2 | | 2 | |
Szukamy pole przekroju który jest prostokątem jeden z boków jest krawędzią podstawy
graniastosłupa
Wiemy że podstawą jest kwadrat o polu 25
P
p=a
2 ⇒ a =
√25=5
teraz szukamy dłuższy bok prostokąta
P
b=480= 4*a*b( 4 prostokąty tworzą powierzchnię boczną)
| | 480 | |
480= 4*5*b ⇒ b= |
| = 24 |
| | 20 | |
Teraz patrzymy na trójkąt prostokątny który tworzą krawędz boczna krawędz podstawy oraz szukany
bok prostokąta przekroju
Tw.Pitagorasa : c
2=a
2+b
2= 25+576=601 ⇒c=
√601
Pole przekroju :
P= 5*
√601= 5
√601
Sprawdz czy nie popełniłem jakiegoś błędu

pozdrawiam
26 wrz 21:08
Stachu: oj szukałem i wogóle nie to znalazłem

ale powinieneś już sam obliczyć sinus bo masz wszystko

26 wrz 21:10


 pozdrawiam
pozdrawiam
 ale powinieneś już sam obliczyć sinus bo masz wszystko
ale powinieneś już sam obliczyć sinus bo masz wszystko
