Styczne Stokrotka: Napisz rownania osi symetrii figury, ktora jest suma dwoch okregow o rownaniach (x+3)²+(y−3)²=4 (x−2)²+(y+4)²=4

Stokrotka: Pomoze ktos?

Stokrotka: pomocy

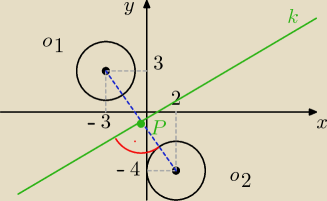
Trivial: o₁: (x+3)²+(y−3)² = 4 o₂: (x−2)²+(y+4)² = 4 Zauważ na początku bez żadnego liczenia, że okręgi mają równe promienie, a więc zawsze istnieje prosta, względem której są symetryczne. S₁ = (−3,3), S₂ = (2,−4), R = 2 ← rysujemy. Teraz zauważmy, że ta prosta, nazwijmy ją k, przechodzi przez punkt P i jest prostopadła do prostej S₁S₂. Punkt P jest środkiem odcinka S₁S₂. Jako, że nie mamy do czynienia z prostymi 'pionowymi', policzymy współczynnik kierunkowy prostej S₁S₂ (niebieska przerywana).

	S2,y−S1,y		−4−3		7
aS1S2 =		=		= −		.
	S2,x−S1,x		2+3		5

Prosta k ma współczynnik kierunkowy równy:

	1		5
ak = −		=		.
	aS1S2		7

Teraz wyliczymy punkt P, który jest środkiem odcinka S₁S₂:

	S1,x+S2,x		S1,y+S2,y		1		1
P = (		,		) = (		, −		).
	2		2		2		2

Prosta k ma współczynnik kierunkowy a_k i przechodzi przez punkt P − punkt P spełnia równanie prostej k. k: y = ax + b

	1		5		1
−		=		*		+ b
	2		7		2

...

	6
b = −		.
	7

	5		6
Odpowiedź: Szukana oś symetrii ma równanie y =		x −		.
	7		7

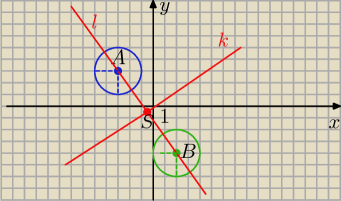Eta: 1 symetralna to prosta AB 2 symetralna to symetralna odcinka AB ( czyli prostoadła do pr. AB i przechodzi przez S −−środek odcinka AB Wiem,że już teraz dasz radę powodzenia

Trivial: Witaj Eto.

Eta: Wrrrrrrrrr Trivial ..... na darmo męczyłam się z rysunkiem

Trivial: Też miałem kratkę rysować, ale stwierdziłem, że za długo zejdzie.

Eta: Trivial ..... a gdzie równanie drugiej symetralnej ?

Eta: tzn. drugiej osi symetrii

Trivial: Zapomniało mi się. Współczynnik jest, to można już doliczyć.

Eta: