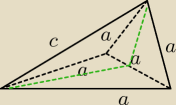
Podstawą ostrosłupa jest trójkąt równoboczny gdzie... Truman: Podstawą ostrosłupa jest trójkąt równoboczny gdzie długość boku wynosi "a" a jedna z ścian pada pod kątem prostym na płaszczyznę podstawy i również jest trójkątem równobocznym identycznym jak podstawa. Znajdź pole powierzchni tego ostrosłupa. Ja chciałem robić to tak(a może się mylę): 1. Wyliczam krawędź "c" z twierdzenia Pitagorasa:

	a√3		a√3
(		)2 + (		)2 = c2
	2		2

2. Wyliczam ze wzoru Herona pole trójkąta bocznego:

2a+c
	=p
2

P_trójkąta=√p*(p−a)²*(p−c) 3. Pole boczne to będzie:

	a2√3
Pb=		+2*Ptrójkąta
	4

Czy to jest dobry sposób czy inaczej da się to zadanie zrobić? Może coś ważnego pominąłem lub nie zauważyłem?

Basia: bardzo dobrze −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− inny sposób na podpunkt 2 istnieje, ale chyba niewiele prostszy to jest trójkąt równoramienny: podstawa c, ramiona a,a liczę z Pitagorasa wysokość i pole z klasycznego wzoru

Basia: a i w (3) mały błąd masz policzyć P_c

	a2√3
Pc = 2*		+ 2*Ptr.c−a−a
	4

Truman: Tzn chodzi mi o pole powierzchni bocznej nie o całkowite dlatego tylko 1 trójkąt równoboczny brałem pod uwagę. Co do podpunktu 2 to właśnie się zastanawiałem nad tym Basiu To by było:

	c
hs=√a2−(		)2
	2

	c   c*√a2−( )2   2
i pole: P=
	2

Dziękuję za wskazówkę i pomoc. Pozdrawiam!