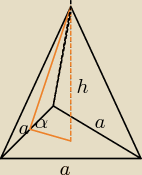
oblicz pole Elena: pilnie potrzebuję na poniedziałek ! W ostrosłupie prawidłowym trójkątnym o wysokości długości h ściany boczne są nachylone do płaszczyzny podstawy pod kątem o mierze α . Oblicz objętość i pole powierzchni całkowitej tego kręgosłupa .

ICSP: hi hi hi znów kręgosłup

ICSP: http://pl.wikipedia.org/wiki/Kr%C4%99gos%C5%82up

Elena: ostrosłup

ICSP: Zostawimy Godziowi

Elena: za dużo tej matmy na dziś poddaję się oczywiście chodzi o objętość i pole powierzchni całkowitej ostrosłupa

ICSP: Godziu jesteś?

Truman: Ja bym to tak zrobił: 1. Liczę wysokość "H" ostrosłupa:

H
	= sinα
h

H = sinα*h 2. Liczę krawędź "a" podstawy:

a√3   6
	= cosα
h

a√3
	= cosα
6h

a√3 = 6h*cosα

	6h*cosα		√3
a =		*
	√3		√3

	6√3h*cosα
a =
	3

a = 2√3h*cosα 3. Wyliczam objętość:

	1		(2√3h*cosα)2*√3
V =		*		*sinα*h
	3		4

	12h2*cos2α*√3*sinα*h
V =
	12

V = √3*h³*cos²α*sinα −−−−−−−−−−−−−−−−−−−−−−−−− Teraz pole powierzchni całkowitej:

	1		(2√3h*cosα)2*√3
Pc = 3*		*(2√3h*cosα)*h+
	2		4

P_c = 3√3*h²*cosα+3√3*h²*cos²α P_c = 3√3*h²*cosα*(1+cosα) Nie jestem pewien czy to dobrze obliczyłem. Są ode mnie lepsi fachowcy i niech oni sprawdzą czy to co napisałem się nadaje Pozdrawiam!

Elena: a która to jest zależność funkcji trygonometrycznej ? czy tutaj korzystamy z tg α ?