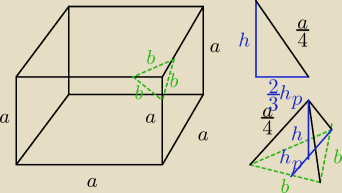!
z odciętego naroża powstanie ostrosłup prawidłowy o podstawie trójkąta o boku (b) i
krawędzi bocznej a4
trzeba policzyć objętość tego ostrosłupa. Takich ostrosłupów będzie prawdopodobnie osiem.
Od objętości całego sześcianu odjąć 8 objętości ostrosłupa i po krzyku. 
b2 = (a4)2 + (a4)2
| a√2 | ||
b = | → krawędź podstawy ostrosłupa (zielonego)
| |
| 4 |
| b√3 | a√6 | |||
hp = | = | → wysokość podstawy ostrosłupa
| ||
| 2 | 8 |
| a | a√6 | a | ||||
h = √( | )2 − ( | )2 = | *√3 → wysokość ostrosłupa
| |||
| 4 | 12 | 12 |
| b2√3 | a2√3 | |||
Pp = | = | → pole podstawy ostrosłupa
| ||
| 4 | 32 |
| a3 | ||
V = 13Pp*h = | → objętość ostrosłupa
| |
| 384 |
| 47 | ||
Vs = a3 − 8*V = | a3 → objętość sześcianu po obcięciu | |
| 48 |
ale bez paniki
trzeba policzyć powierzchnie boczną ostrosłupa odciętego z naroża, pomnożyć przez 8 i
odjąć od całkowitej powierzchni sześcianu a później dodać 8 podstaw tego ostrosłupa
Pb = 14a*14a*32*8 = 34a2 (−)
| a2√3 | a2√3 | |||
Pp = | *8 = | (+)
| ||
| 32 | 4 |
| 21 + √3 | ||
Ps = 6a2 − Pb + Pp = a2( | ) → powierzchnia sześcianu po obcięciu | |
| 4 |
objętość ściętego naroża można wyznaczyć też tak:
H−−wysokość ostrosłupa
| 1 | a | a2 | ||||
PΔABC= | *( | )2= | ||||
| 2 | 4 | 32 |
| 1 | a3 | |||
V= | PΔABC*H= ...... = | |||
| 3 | 384 |