Rozwiąż nierówność AroSteel: 1/x² > 1

Kejti:

1
	>1 /*x2
x2

1>x² x<1 x≠0

Vizer:

1
	−1>0
x2

1−x2
	>0
x2

−x²(x²−1)>0 −x²(x−1)(x+1)>0 x²(x−1)(x+1)<0 x∊(−1,0) ∪ (0,1)

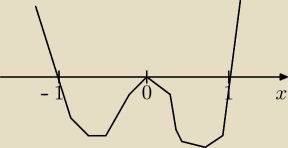
AroSteel: Dzięki wielkie chodziło mi o ten wykres bo nie wiedziałem, czy jak D: R\{0} i w rozwiązaniu pojawia się x=0 to czy omijam to zero, czy przechodze przez nie, a tu się okazuje, że odbijam się od niego i dalej jestem na liczbach ujemnych.

ICSP: po co sobie utrudniać tka życie?

1
	> 1
x2

D : x ∊ R\{0} Zauważamy że mianownik jest zawsze > 0 i przemnażamy przez x² 1 > x² ⇔ x² − 1 < 0 ⇔ (x−1)(x+1) < 0 ⇔ x ∊ (−1;1)/{0}

Kejti: no tak..to by było zbyt proste..

Vizer: No fakt ICSP nie pomyślałem

ICSP: ale Vizer twoje rozwiązanie również jest poprawne Kejt dziś ty chyba wygrasz konkurs na głupotę dnia

Kejti: dzięki. żeby to pierwszy raz..

Kejti: ale to pewnie przez to, że j.polski odrabiam..to mnie odmóżdża..