granica nx: Witam czy mógłby ktoś pokazac granice ciągu geometrycznie bo z suchej definicji niewiele rozumiem

Trivial: Która definicja cię interesuje?

Trivial: W sumie dla ciągów jest chyba tylko jedna...

nx: ta ogólna z otoczeniem liczby g i tym ε nie bardzo mozna załapac o co kaman

Trivial: Jeśli nikt inny nie wyjaśni, to jak wrócę później to pomogę.

nx: Ok mi sie nie spieszy

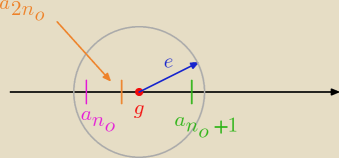
Trivial: Najpierw sama definicja granicy właściwej Def. Liczba g∊R jest granicą właściwą ciągu (a_n), gdy: ∀ε>0 ∃n₀∊ℕ : ∀ n≥n₀ |a_n − g| < ε. Ozn. g = lim_n→∞ a_n. Wyjaśnienie: Dla dowolnie małej wartości ε (czyli z dowolnie wysoką dokładnością) wszystkie wyrazy a_n zaczynając od pewnego n₀ mają wartość odległą od g mniej niż ε − leżą w otoczeniu g − U(g,ε). (ε na rysunku zaznaczony jest przez e)

Trivial: Jak masz pytania jeszcze to pytaj, bo nie wiem co jest niejasne.

Trivial: Główna idea jest taka, że a_n osiąga wartości dowolnie bliskie g, ale nigdy równe.

nx: Teraz juz to rozumiem chodzi o to ze jak cos widze na rysunku to lepiej rozumiem idee tak jak np ocodna funkcji i jej geometryczna interpretacja dzięki wielkie bez tego slepo bym liczył granice ze wzorow wogole nie wiedząc co własciwie licze

nx: edit: "pochodna"