w graniastosłupie prawidłowym czworokątnym o krawędzi podstawy a=6 i krawedzi bo
niki: w graniastosłupie prawidłowym czworokątnym o krawędzi podstawy a=6 i krawedzi bocznej b=5
wyznacz
a miarę kąta nachylenia przekątnej graniastosłupa do podstawy
b) miarę kąta nachylenia przekątnej ściany bocznej do podstawy
c) pole trójkąta którego bokami są przekątne dwóch ścian bocznych i jednej podstawy
d) długość przekątnej graniastosłupa
dero2005:
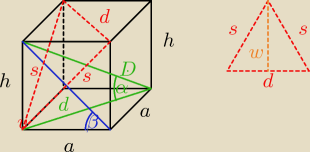
a = 6
h = 5
obliczamy przekątną podstawy d jako przekątna kwadratu
d = a
√2 = 6
√2
obliczmy przekątną graniastosłupa D
D =
√d2 + h2 =
√(6√2)2 + 52 =
√97
wyznaczamy miarę kąta nachylenia przekątnej graniastosłupa do podstawy α
| | h | | 5 | | 5√97 | |
sin α = |
| = |
| = |
|
|
| | D | | √97 | | 97 | |
wyznaczmy przekątą ściany s
s =
√a2 + h2 =
√62 + 52 =
√61
wyznaczamy miarę kąta nachylenia przekątnej ściany do podstawy β
| | h | | 5 | | 5√61 | |
sin β = |
| = |
| = |
|
|
| | s | | √61 | | 61 | |
obliczamy pole trójkąta z punktu c
wysokośc (w) trójkąta
w =
√s2 − (d2)2 =
√(√61)2 − (3√2)2 =
√61 − 18 =
√43
| | d*w | | 6√2*√43 | |
P = |
| = |
| = 3√86 |
| | 2 | | 2 | |