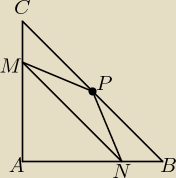
Zadanie optymalizacyjne - funkcja kwadratowa Magdalena: W trójkąt prostokątny równoramienny ABC (|∡BAC| = 90◯) wpisujemy trójkąt MNP tak, że P jest środkiem boku BC, a M ∊ AC, N ∊ AB oraz MN ∥ BC (jak na rysunku). Jak należy wybrać punkty M i N, aby pole trójkąta MNP było największe, jeśli |AB| = |AC| = 4 cm?

Magdalena: Bardzo proszę o jakąś podpowiedź, wzór, cokolwiek.

sushi_ gg6397228: |CM|= |NB|= x |AM|=|AN|=4−x pole PMN= pole AMN + pole PMC + pole PNB

	|MC|* h
pole PMC=		h= 2
	2

	|NB|* h
pole PNB=		h= 2
	2

sushi_ gg6397228: pole PMN= pole ABC− ( pole AMN + pole PMC + pole PNB) zgubilem tam cale pole trojkata

Magdalena: Jak obliczyć, że h = 2?

sushi_ gg6397228: punkt P jest srodkiem BC wiec jak sobie spuscisz wysokosc na AB i AC to zobaczysz ze bedzie 2 ale pewnie nawet nie zrobilas rysunku w zeszycie

Magdalena: Moje próby rozwiązania tego opierały się na szukaniu FUNKCJI KWADRATOWEJ, z której dałoby się rozwiązać to zadanie.

sushi_ gg6397228: podstawa to rysunek

Vax: Można to uzasadnić tak, że po opuszczeniu wysokości z punkt P na AB (niech to będzie punkt X)

	1
dostaniemy trójkąt XBP który jest podobny do ABC w skali
	2

Magdalena: Dziękuję.

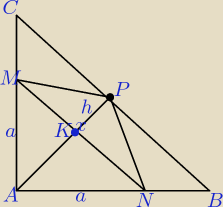
Anna: IABI=IBCI=4cm P_MNPmax= ? IBCI = 4√2, IAPI=IPBI=2√2 IMNI=x, czyli x=a√2 IAK=IKNI (trójkąt podobny do ΔABP) IAKI = IAPI − h = 2√2−h

	x		x
Czyli		= 2√2−h ⇒ h = 2√2−
	2		2

	1		1		x		1
PMNP =		xh =		x(2√2−		) = x√2 −		x2
	2		2		2		4

	1
Powstała funkcja kwadratowa zmiennej x: P(x) = −		x2+√2x
	4

	−b		−√2
Obliczamy xw=		=		= 2√2 (tutaj "a" to nie to "a" co na
	2a		1   −   2

rysunku) Zatem maksymalne pole jest dla argumentu x=2√2. Teraz wystarczy obliczyć długość odcinka IANI=a, bo w tej odległości od punktu A należy umieścić punkt N (także punkt M od punktu A).

	x		2√2
a=		=		= 2 [cm]
	√2		√2

Odp. Pole ΔMNP będzie największe, jeśli punkty M i N będą umieszczone w odległości 2cm od punktu A.