Trivial:
Równanie parametryczne prostej wygląda tak:
x = A +
ut, t∊R
gdzie:
x − wektor−punkt należący do prostej,
A − dowolny punkt należący do prostej,
u − wektor styczny do prostej,
t − parametr.
Wyjaśnienie:
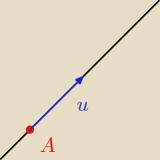
Punkty leżące na prostej spełniają powyższe równanie wektorowe. Wektor
u jest styczny do
prostej. Zaczepiając go w punkcie A możemy otrzymać dowolny punkt na prostej poprzez mnożenie
wektora
u przez liczby (parametr t). Poszczególne kombinacja
ut dają nam
poszczególne punkty leżące na prostej. t∊R więc możemy otrzymać dowolny punkt.

 Równanie parametryczne prostej wygląda tak:
x = A + ut, t∊R
gdzie:
x − wektor−punkt należący do prostej,
A − dowolny punkt należący do prostej,
u − wektor styczny do prostej,
t − parametr.
Wyjaśnienie:
Punkty leżące na prostej spełniają powyższe równanie wektorowe. Wektor u jest styczny do
prostej. Zaczepiając go w punkcie A możemy otrzymać dowolny punkt na prostej poprzez mnożenie
wektora u przez liczby (parametr t). Poszczególne kombinacja ut dają nam
poszczególne punkty leżące na prostej. t∊R więc możemy otrzymać dowolny punkt.
Równanie parametryczne prostej wygląda tak:
x = A + ut, t∊R
gdzie:
x − wektor−punkt należący do prostej,
A − dowolny punkt należący do prostej,
u − wektor styczny do prostej,
t − parametr.
Wyjaśnienie:
Punkty leżące na prostej spełniają powyższe równanie wektorowe. Wektor u jest styczny do
prostej. Zaczepiając go w punkcie A możemy otrzymać dowolny punkt na prostej poprzez mnożenie
wektora u przez liczby (parametr t). Poszczególne kombinacja ut dają nam
poszczególne punkty leżące na prostej. t∊R więc możemy otrzymać dowolny punkt.
