Ostrosłup prawidłowy czworokątny
deith:
Hey bardzo proszę o pomoc w tym zadaniu
Pozostale mam podobne wiec prosze tylko o wasze
spostrzezenia itp
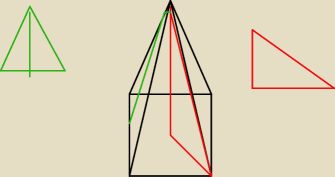
W ostrosłupie prawidłowym czworokątnym długośc krawedzi podstawy jest rowna 4
√2 a krawedzi
bocznej 5cm.Oblicz:
a) wysokosc tego ostroslupa kolor czerwony wyliczam z pitagorasa ?(przekatna kwadratu ma
a
√2 wiec (1/2
√2)
2+h
2=5
2 ?
b) wysokosc sciany bocznej poprowadzoną na krawedz podstawy − h
2+(4
√2/2)
2=5
2 ?
−
c) odleglosc spodka wysokosci ostroslupa do krawedzi bocznej − tego wogole nie rozumiem
20 wrz 14:38
ICSP: Po pierwsze ten rysunek nie jest za przejrzysty.
Po drugie wysokośc ostrosłupa powinno się oznaczać dużą literką H ( co zrobisz jak będziesz też
musiał obliczyć wysokośc ściany bocznej)
Po trzecie (U{1}{2√2)2 + H2 = 25 − co to jest?
20 wrz 14:47
deith: Po trzecie (U{1}{2√2)2 + H2 = 25 − co to jest?
@ to jest ten zielony trojkacik rownoramienny ktory podzielilem na 2 trojkaty prostokatne w
podstawie ma 4
√2/(kreska ulamkowa)2 ramie ma 5cm wiec obliczam z pitagorasa − nie jestem
wogole tego pewien wiec pytam
20 wrz 14:52
ICSP: a = 4
√2
d = 8
4
2 + H
2 = 5
2
H = 3
Nie ma sensu zapisywać zmiennych skoro możemy od razu podstawić i wyliczyć.
20 wrz 14:56
ICSP:
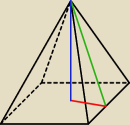
niebieski − wysokość
czerwony − połowa krawędzi podstawy
zielony − wysokość ściany bocznej.
Skoro już wyliczyłeś wysokość ostrosłupa to użyj jej
20 wrz 15:00
roman: wg mnie h= 3
20 wrz 15:00
roman: szybcy i wściekli ....
20 wrz 15:01
deith: dzieki a co do pozostalych a,c?
20 wrz 15:01
deith: ok wielkie dzikei
20 wrz 15:02
roman:
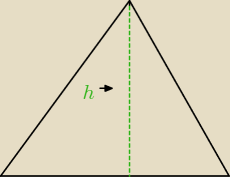
to chcesz wyliczyć w b)
20 wrz 15:05
roman: >?
20 wrz 15:07
deith: tak
20 wrz 15:07
roman: czyli dół tego rysunku ma 4
√2 a my potrzebujemy tylko jej połowy
20 wrz 15:08
roman: jego*
20 wrz 15:08
roman: h=√17
20 wrz 15:09
deith: tez mi tak wyszlo
20 wrz 15:10
deith: tylko zastanawialem sie jak bedzie z a i c
20 wrz 15:11
roman: w c) wydaje mi się że chodzi o odl od tego miejsca z którego długość h jak schodzi z góry w dół
i jak się znajdzie na samym dole i dotknie podłoża tej bryły to właśnie od tego miejsca do
krawędzi potrzebujemy odległości ale to też można obliczyć Pitagorasem ....
20 wrz 15:11
deith: w sensie podpunktow w zadaniu
20 wrz 15:11
roman: no a ) już masz ICSP Ci zrobił ... ( h = 3 )
20 wrz 15:12
może: zazaraz Ci narysuje c)
20 wrz 15:14
deith: dzieki za pomoc roman duzo mi pomogles
20 wrz 15:16
może:
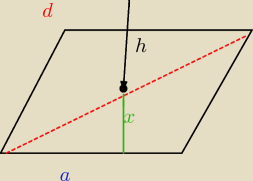
więc potrzebujemy nasza przekątna która już obliczyliśmy jest ona równa
d=8 ale my potrzeujemy połowe jej wiec 4
| | 1 | | 2√2 | |
no i teraz połowę a chili |
| 4√2 = |
|
|
| | 2 | | 2 | |
no i Pan Pitagoras ...
20 wrz 15:17
może: =
roman :
20 wrz 15:18
roman: wiesz mam nadzieje że jest db ....
20 wrz 15:19
deith: wlasnie dlaczego przekatna ma 8 ?
20 wrz 15:19
20 wrz 15:20
roman: a = 4
√2
d= a
√2
podstawiasz a i jeszcze ten nasz
√2
i mamy
d= 4
√2*
√2 = 4*2=8
20 wrz 15:21
deith: okey zacmienie ..
spoko tez mi sie wydaje ze jest dobrze jescze raz dzieki za pomoc i do
kolejnego rozwiazywania zadan..
20 wrz 15:24
roman: wątpie jestem tu gościnnie ...
20 wrz 15:26