wartość bezwzględna ddd: wartość bezwzględna z

2x − 3
x − 3

jest mniejsza równa 1

ddd:

2x − 3
	< 1
x − 3

2x−3<x−3 x<0

2x − 3
	>−1
x − 3

2x−3>−x+3 x>2 wynik powinien miescic się w przedziale (0,2) rachunkowo jako wynik otrzymałem całą resztę. Dlaczego?

Anna: piszę

Anna: To nie tak. Nierówności nie można mnożyć obustronnie przez mianownik.

2x−3
	− 1 < 0
x−3

Sprowadzamy lewą stronę do jednego ułamka:

2x−3−(x−3)
	< 0
x−3

x
	< 0
x−3

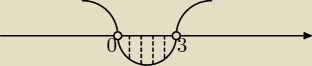
Iloraz zamieniamy na iloczyn: x*(x−3) < 0 Wyznaczamy miejsca zerowe z każdeko czynnika: x=0, x=3 Wykonujemy wykres tzw. "wężyk" (zawsze od strony prawej, tym razem od góry) i odczytujemy rozwiązanie ( gdzie wykres przyjmuje wartości ujemne): x ∊ (0,3)

Anna: dopisuję

Anna:

	2x−3		2x−3
I		I < 1 ⇔ −1<		< 1
	x−3		x−3

ddd: Wielkie dzięki

Anna: Zatem trzeba rozwiązać jeszcze lewą część nierówności i wyznaczyć część wspólną rozwiązań obu nierówności pojedynczych.

ddd: Dzięki , już rozumiem

Anna:

2x−3
	> −1
x−3

2x−3
	+ 1 > 0
x−3

2x−3+x−3
	> 0
x−3

3x−6
	>0
x−3

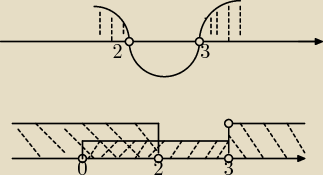
3(x−2)(x−3)>0 ⇒ m. zer.: x+2, x=3 Na podst. wykresu: x∊ (−∞,2)U(3,∞) Część wspólna z obu wykresów, to: x∊(0,2)