Monotoniczność ciągów liczbowych. panna_waga: Mam jeszcze 2 przykłady. Zrobiłam je, ale wątpliwości są; chciałabym, żeby ktoś zobaczył i sprawdził czy ok, a jak nie ok, to co nie tak. Z góry wielkie dzięki a)

	n
bn =
	2n + 1

	(n+1)		(n+1)		(n+1)
bn+1 =		=		=
	2(n+1)+1		2n+2+1		2n+3

	(n+1)		n		2n2+3n+2n+3−2n2−3n
bn+1 − bn =		−		−
	2n+3		2n+1		(2n+3)(2n+1)

Ciąg rosnący chyba, ale mógłby ktoś naprowadzić mnie dlaczego b) c_n = n²+3n c_n+1 = (n+1)² + 3n = n²+1+3n c_n+1 − c_n = (n²+1+3n) − (n²+3n) = n²+1+3n−n²+3n = 1 I jest to ciąg rosnący. [?]

sushi_ gg6397228: a) jak zrobisz wspolna kreske, to musis sie cos skrocic w liczniku b) masz parabole n(n+3) wiec od razu widac ze dla n∊N₊ jest rosnacy

panna_waga: a no, ja niechcacy nie dokonczylam tego przykladu a).. ciag dalszy jest taki, znaczy taki jest efekt koncowy (u mnie):

	2n+3
a)
	(2n+3)(2n+1)

A o b) musisz wybaczyć, ale nie wiem o czym mówisz znaczy, nie wiem o co chodzi z tą parabolą chcesz to możesz się lekko rozpisać, jeśli nie to tylko napisz czy dobrze.

sushi_ gg6397228: a) mi wyszlo inaczej b) (a+b)² −... wzor skroconego mnozenia

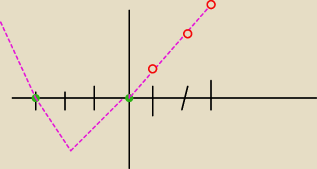
sushi_ gg6397228: wykres rozowy f(x)=x(x+3) kołka czerwone wykres f(n)=n(n+3)

panna_waga: a) to możesz mnie naprowadzić gdzie ja ten błąd zrobiłam? bo zanim to tu wstawiłam, bo kilka razy robiłam i tak samo wychodziłam.;. musiałam więc się gdzieś pośliznąć, ale nie mam pojęcie gdzie.. b) tylko nie wzor skroconego mnozenia, ojeny gdzieś mam go użyć w tym przykładzie? czy jest on jednak dobrze roziwązany?

panna_waga: ja noga z matmy i mało czaje, ale wieeeelkie dzięki za fatygę, może jak posiedzę dłużej przy tym to ogarnę.

sushi_ gg6397228: a)to zapisz jeszcze raz odejmowanie ulamkow b) c_n+1= (n+1)² +3(n+1) kolor czerwony wzor skroconego mnozenia

panna_waga:

	1
ok. a) zrobiłam jeszcze raz i wyszło mi		− dobrze już zrobiłam, czy
	(2n+1)(2n+3)

sknociłam znowu coś?

sushi_ gg6397228: mianownik zawsze dodatni, licznik tez, wiec b_n+1−b_n >0 c. rosnacy

panna_waga: b) po użyciu wzoru skróconego mnożenia: c_n+1 = (n+1)² + 3(n+1) = n²+2*n*1+1+3n+3 = n² + 1 + 3n + 3 = n²+5n+4 c_n+1 − c_n = n²+5n+4−n²+3n = 8n+4 I jak? Jakaś nadzieją we mnie jest jako matematyczki?

panna_waga: czyli dobrze a) już ogarnęłam?

sushi_ gg6397228: c_n+1 − (c_n) zapomnialas o nawiasach i bład w odejmowaniu

sushi_ gg6397228: do a) dalej nie miales zastrzezen w poscie o 17.06

panna_waga: dzięki za naprowadzenie do tego a) a jeśli chodzi o c) to to ma być tak (efekt): 2n+4 ?

sushi_ gg6397228: 2n+4>0 czyli c rosnacy

panna_waga: tak myślałam, że to rosnący, ale nie byłam pewna czy w ogóle dobrze to rozwiązałam. ojacie, wielkie dzięki! żebym ja taki mózg miała dzięki jeszcze raz.

sushi_ gg6397228: to juz bylo widac po rysunku, ktory zamiescilem wczesniej