okrąg kamil: w okrag x²+y²=20 wpisany jest trójkąt równoramienny prostokątny. wierzchołek kąta prostego tego trójkąta ma współrzędne (2,4). wyznacz współrzędne pozostałych wierzchołków.

req: skorzystaj z tego że prosta y=ax+b przechodzi przez punk (2,4) oraz tego że wspołczynniki "a" prostych których szukasz muszą spełniać równanie a₁*a₂=−1 , no i oczywiście długości muszą mieć takie same

kamil: niestety, ale nie wiem jak to zrobc.

req: oprócz tego przeciwprostokątna to jest średnica naszego okręgu , prosta zawierająca średnice przechodzi przez środek naszego koła. Oblicz odleglość środka od naszego punktu (2,4) i narysuj sobie to

req: prosta przechodząca przez środek i punkt (2,4) to y=2x

	1
prosta prostopadła do tej prostej to y=−		x
	2

teraz tylko punkty wspólne tej prostej z okręgiem , trzeba rozwiązac układ równań

	1
y=−		x
	2

y²+x²=20 , można jeszcze prosciej

req: przepraszam , zapedziłem się

	1
4=−		2+b to jest ta nasza prosta
	2

b=5

	1
y=−		x+5
	2

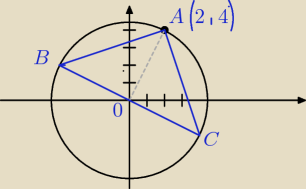
dero2005: liczę współczynnik a prostej AO

	4−0
aAO =		= 2
	2−0

liczę współczynnik kierunkowy prostej BC prostopadłej do OA

	−1
aBC =		= −12
	2

liczę równanie prostej BC przechodzącej przez punkt O(0,0) y_BC = a_BC(x − x_O)+ y_O y_BC = −¹₂(x− 0) + 0 = −¹₂x liczę punkty B i C porównuję równanie prostej BC i równanie okręgu −¹₂ x= √20− x² |^{2 1}₄x² = 20−x² x₁ = −4 x₂ = 4 y = −¹₂x y₁ = 2 y₂ = −2 B (−4. 2) C (4, −2)

Adian: Powyżej wszystko dobrze, tylko mało wytłumaczone i niektórzy nie rozumieją, więc: Współczynnik prostej AO liczymy przez podstawienie pod równanie funkcji liniowej y=ax+b wspolrzednych punktow A=(2,4) i 0=(0,0). Tak więc: 0=a*0+b oraz 4=2*a +b. Wychodzi jak to napisał dero: y=2x. Wzór na współczynnik kierunkowy(a) prostej prostopadłej to a₁*a₂=−1 z czego wynika że a₂ = −1/a₁ czyli −1/2. Z powyższego wiemy że prosta BC wyraża się funkcją y=−1/2x + b, a po podstawieniu współrzędnych punktu 0=(0,0) zauważamy że b=o czyli y=−1/2x. Szukamy punktów wspólnych okręgu x² + y*2 = 20 i prostej y=−1/2x. Najprościej podstawić pod y z równania okręgu wartość funkcji y = −1/2x czyli: x² + (−1/2x)² = 20 i tu po odpowiednich przekształceniach możemy dotrzeć ławo do postaci dero2005 i po rozwiązaniu wychodzi rzeczywiście x₁=−4 a x₂=4 a więc y₁=2 a y₂=−2 Wytłumaczenie na prośbę kogoś kto nie mógł załapać.

Hhh: a skąd wiedzieć ze punkt S leży na punkcie 0,0 nie mając rysunku?

5-latek: Np stad Rownanie okregu w postaci kanonicznej jest takie (x−x_s)²+(y−y_s)²=r² gdzie x_s i y_s to wspolrzedne srodka okregu masz takie rownanie x²+y²=20 To rownanie mozemy zapisac tak (x−0)²+(y−0)²=20 jakie masz tu wspolrzedne srodka okregu? Odczytaj je sobie glosno