Pole i wysokość graniastosłupa prawidłowego czworokątnego Łaciaty: Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 50 cm2. Przekątne ścian bocznych tego graniastosłupa tworzą kąt o mierze 45 stopni. Oblicz długość: a) krawędzi podstawy b) wysokości podstawy. Podpunkt a rozwiązany. Natomiast z b nie potrafię sobie poradzić. Za pomoc z góry dziękuję

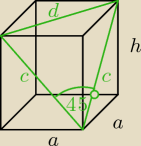
dero2005: P_p = a² = 50 cm² a = √50 = 5√2 cm d = a√2 = 5√2*√2 = 20 cm tw cosinusów d² = c² + c² − 2c²*cos 45^o 20² = 2c²(1 − cos 45^o)

	√2
400 = 2c2(1 −		)
	2

	2−√2
200 = c2*
	2

c² = 400 − 200√2 tw Pitagorasa h = √c² − a² = √400−200√2−400 = √200√2 cm w punkcie b) chodzi o wysokość graniastosłupa chyba bo nie ma takiej wielkości jak wysokość podstawy w graniastosłupie czworokątnym

Łaciaty: Dziękuje bardzo za pomoc. Oczywiście w punkcie b chodzi o wysokość graniastosłupa (błąd podczas pisania).