Z punktu P Jerzy: Z punktu P poprowadzono styczne PA i PB do okręgu o(O, r) w punktach A i B. Wykaż, że jeśli |<)APB| = |<)AOB|, to czworokąt PAOB jest kwadratem.

Jerzy: up

sushi_ gg6397228: zrob rysunek

Jerzy: zrobiłem i zaciąłem się w pewnym momencie

sushi_ gg6397228: to go tutaj pokaz

Jerzy: nie xd

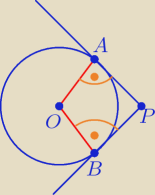
rumpek: [...] Jerzy demotywujesz bardziej niż demotywatory ... Rysunek masz powyżej, przydane informacje: Narysujesz u siebie w zeszycie bardziej "kwadratowy" ten kwadrat Z zadania wiesz, że ∡APB = ∡AOB. Wiemy także, że prosta jest styczna do okręgu, czyli 90^o. (na rysunku kąt prosty przy A) Suma kątów w czworokącie to 360^o, czyli: 90^o + 90^o + ∡APB + ∡AOB = 360^o ∡APB + ∡AOB = 180^o ∡APB + ∡APB = 180^o (są równe więc podstawiam ze AOB <= APB) 2∡APB = 180^o / : 2 ∡APB = 90^o, czyli ∡AOB = 90^o. Kąty mają po 90^o zatem jest to kwadrat.

Jerzy: dziękuję serdecznie

Mateusz: rumpek nie tylko kwadrat jest kwadratowy

Jerzy: ej ale prostokąt tez ma kąty 90^o; tu chyba trza udowodnić równe boki?

Jerzy: no własnie Mateusz xD

Jerzy: tak w ogóle rozwiązanie rumpka jest dobre?

rumpek: Po części... ukazane jest ze katy 90^o A po drugie musisz udowodnic jeszcze ze ma równe boki, nie jest to trudne bo |AO| = |BO| (promienie) reszte nie jest juz trudno zrobic

Jerzy: oo git