funkcja
ciekawy: jest roznica czy powiemy dwa miejsca zerowe dodatnie czy dwa pierwiastki dodatnie?
17 wrz 13:26
ciekawy: ?
17 wrz 13:56
Gustlik: Żadna.
17 wrz 13:56
AS: Moim zdaniem jest taka różnica;
Gdy znalezione rozwiązania znajdują się na osi Ox to są to miejsca zerowe,
w przeciwnym razie pierwiastkami.
Dla równania x2 − 4 = 0 , x1 = −2 i x2 = 2 są miejscami zerowymi (−2,0) i (2,0)
Dla równania 5*x − 4 = x + 6 , x = 5/2 , jest to pierwiastek,
lewa strona równania ma wartość 17/2 (a nie 0) , prawa strona również 17/2
17 wrz 15:31
Gustlik: Dla równań − tak, ale dla funkcji − nie ma różnicy. Ale nawet dla równań też może nie być
różnicy, np. równanie x=2 można przekształcić do postaci x−2=0, wtedy jak podstawisz x=2,
otrzymasz 0=0.
17 wrz 16:04
AS: Tak,ale po przekształceniu staje się zerem.Ogólnie biorąc,pierwiastkiem
jest każda liczba spełniająca równanie (układ równań) a miejscem zerowym
nie każda.
17 wrz 16:32
ciekawy: pytam sie bo majac zadanie z parametrem m w odpowiedzi spotkalem sie z czyms takim: gdy ma dwa
miejsca zerowe dodatnie Δ>0,a gdy ma dwa pierwiastki dodatnie Δ≥0 dlatego pytam?
17 wrz 21:22
ciekawy: ?
17 wrz 21:41
Jack:
"dwa miejsca zerowe" powinno być dla Δ≥0 (bo nie ma zastrzeżenia że chodzi o dwa różne miejsca
zerowe) + inne warunki.
Mnie się wydaje, że różnica tkwi w definicji, lecz tw. Bezouta pozwala nam na stwierdzenie że
zachodzi równoważność znaczeniowa między tymi pojęciami.
(bazuję na tej def.
http://pl.wikipedia.org/wiki/Wielomian#Pierwiastki )
17 wrz 22:10
Jack:
AS, potrafisz podać przykład pierwiastka równania nie będącego miejscem zerowym tego
równania (potraktowanego już jako pewna funkcja)?
17 wrz 22:12
AS:
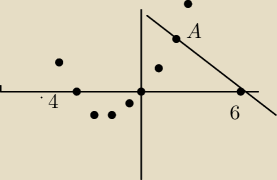
x
2 + 4*x = 6 − x , A(1,5)
18 wrz 09:38
AS: Dopisek.
Moim zdaniem miejsce zerowe zachodzi dla równania postaci f(x) = 0
a pierwiastek dla równości f(x) = g(x)
18 wrz 09:48
Jack:
to ja przerzucając wszystkie wyrażenia na jedną stronę, otrzymuję równanie pewnej funkcji i mam
miejsce zerowe równe pierwiastkowi (i zawsze będą sobie równe, o ile istnieją).
A tę równość zawsze można potraktować jako f(x)−g(x)=0, i przyjąć h(x)=f(x)−g(x), wtedy h(x)=0.
Ja zasadniczo nigdy nie rozróżniam tych pojęć.
18 wrz 11:00
Trivial: Miejsce zerowe jest dowolnej funkcji, a pierwiastek wielomianu. No nie?

18 wrz 11:42
Mateusz:
A wielomian nie jest funkcją

18 wrz 11:48
Trivial: Jest. Ale nie mówi się pierwiastek funkcji. Przynajmniej nie spotkałem się.
18 wrz 12:01
Trivial:
To i tak jest jedno i to samo...
18 wrz 12:02
Mateusz:
Ja tym bardziej się z czyms takim nie spotkałem.
18 wrz 12:08
 x2 + 4*x = 6 − x , A(1,5)
x2 + 4*x = 6 − x , A(1,5)

