Oblicz nierónosć. ona: Rozwiaż nierówność: 3x³−x²−3x+1≤x−1/3

Eta:

	1
W(		)=....... =0
	3

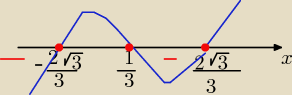
	1
dzieląc ( np. schematem Hornera) W(x) : ( x−		)
	3

	4
3 −1 −4
	3

1		4
	1 0 −
3		3

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 3 0 −4 0

	1
(3x2−4)(x−		)≤ 0
	3

	2√3		2√3		1
(x−		)*( x+		)*( x−		)≤ 0
	3		3		3

x€ .............

Jack: 3x³−x²−3x+1≤x−1/3 3x³−x²−3x+1−x+1/3≤0

	1		1		1
3x2(x−		)−3(x−		)−(x−		)≤0
	3		3		3

	1
(x−		)[3x2−3−1]≤0
	3

.... .... dalej jak u Ety, niemniej bez dzielenia.

Eta: Wieczorem zaraz Gustlik skomentuje : " skąd wiedziałeś ,że tak należy pogrupować ?"

Jack: taa... dlatego nie odpowiadam na jego zaczepki. Trzeba umieć widzieć, skoro się już patrzy!

Jack: (a poza tym skąd on miałby wiedzieć, że należy podzielić akurat przez x−1/3, tzn. jak szybko odszukać pierwiastek )

Gustlik: 3x³−x²−3x+1≤x−1/3 /*3 9x³−3x²−9x+3≤3x−1 9x³−3x²−9x+3−3x+1≤0 9x³−3x²−12x+4≤0 3x²(3x−1)−4(3x−1)≤0 (3x²−4)(3x−1)≤0 (√3x−2)(√3x+2)(3x−1)≤0 Dalej jak u Ety. P.S. Jack, ja Cię nie zaczepiam, ale zdarzało Ci się, że rozwiązywałeś, metodą grupowania wyrazów takie wielomiany, które na początku zawierały współczynniki "ni z gruszki ni z pietruszki". Nie neguję tej metody, ale gwarantuję Ci, że jeden uczeń na milion wpadnie na to, jak porozbijać wspólczynniki tam, gdzie nie widać zależności, np. proporcji między nimi. Do takich wielomianów najlepszy jest Horner − szybko, sprawnie i bez czasochłonnego wymyślania liczb.