monotoniczność adrian:

(x2−2x+1)
(x2−4)

prosze o info jak wyciągnąć pochodną?doszedłem do momentu gdzie wyszło mi

	4−2x3=2x2
	(x2−4)2

sądzę, że to zły wynik i zastanawiam się czy nie policzyć wcześniej z delty bo przy wykorzystaniu wzoru:

(x)'*(y)−(x)*(y)'
(y)2

i w pewnym momencie otrzymałem:

(2x−2)*(x2−4)−(x2−2x+1)*2x
(x2−4)2

czy w tym momencie nie powinienem liczyć z delty?: (x²−2x+1)*2x i powinienem otrzymac 3 punkty na wykresie? x₁ i x₂ i x=−2

ICSP:

(x−2)2		x−2
	=
(x−2)(x+2)		x+2

ICSP:

x−2		x+2 − 4		−4
	=		=		+ 1
x+2		x+2		x+2

	−4
Wykres funkcji y =		przesuwasz o dwie jednostki w lewo oraz o jedną jednostkę w góry.
	x

ICSP: już śpię

(x−1)2
(x−2)(x+2)

ICSP:

(2x − 2)(x2−4) − (x−1)2*(2x)
(x2−4)2

licznik: 2(x−1)x² −4 − (x−1)² * 2x

Jack: zauważasz, że mianownik jest zawsze >0 stąd szukasz pierwiastków w liczniku i uwzględniając dziedziną piszesz przedziały gdy jest on >0 oraz <0.

ICSP: (x−1)(2x² − 8 − 2x² + 2x) = (x−1)(2x − 8) = 2(x−1)(x−4) − koniec licznika czyli pochodna to :

2(x−1)(x−4)
(x2−4)2

Na moje trzy pierwsze posty to nawet nie patrz bo źle przeczytałem wzór funkcji.

ICSP: i zapomniałem o nawiasie dla x² − 4 w poście z 22:36

adrian:

(2x−2)*(x2−4)−(x2−2x+1)*2x
(x2−4)2

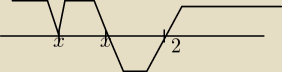
bardzo proszę o dokończenie zadania...bo już się zakręciłem. wykładowca zaznaczył mi na kolokwium, że powinienem obliczyć z Δ (delty) : (x²−2x+1)*2x i powinienem otrzymac 3 punkty na wykresie? (x²−2x+1)*2x (x₁ , x₂ ) 2x=0 ⇒x=−2 nie wiem jak opisac wykres: zaczynajac od lewej x₁ póxniej x₂ i −2 jak liczylem deltę to wyszło mi 0 więc licząc x₁ i x₂ też mi wyszło 0 (być może źle policzyłem, nie jestem pewien dlatego chciałbym aby ktoś to sprawdził)

Jack:

	2(x−1)(x2−4)−(x−1)22x
pochodna Twojej funkcji to: f'(x)=
	(x2−4)2

Wobec nieujemnego mianownika przyglądamy się licznikowi. 2(x−1)(x²−4)−(x−1)²2x=2(x−1)[x²−4−x²+x]=2(x−1)(x−4) (a więc na wykresie powinieneś mieć 2 punkty, w obu następuje zmiana znaku, chyba że życzył sobie żebyś zaznaczył punkty wyrzucone z dziedziny − wówczas 4 punkty) Dziedzina to x∊R\{2,−2}, więc nasza pochodna: f'(x)>0 dla x∊(−∞,−2)∪ (−2,1)∪(4,∞) f'(x)<0 dla x∊(1,2)∪(2,4) Stąd x=1 to max i x=4 to min.

adrian: Jack bardzo cię proszę o rozwiązanie od początku do końca tego zadania....patrz pierwszy post. Będę bardzo wdzięczny i reszta odwiedzających również, bo nie widziałem podobnych przykładów na tym forum, tylko dodawanie i odejmowanie a o dzieleniu nikt nic nie pisał.Więc jeszcze raz bardzo proszę o rozwiązanie zadania abym mógł prześledzić.gdy zastosowany będzie wzór skróconego mnożenia lub inny prosze tylko o komentarz, aby było to widoczne.Z góry bardzo serdecznie dziękuję i pozdrawiam

Jack:

	x2−2x+1		(x−1)2		2(x−1)(x2−4)−(x−1)22x
f'(x)=(		)'=(		)'=
	x2−4		x2−4		(x2−4)2

Tu skorzystaliśmy z tego wzoru który zapisałeś w pierwszym post'cie. Co dalej, to już masz zapisane w moim poprzednim wpisie. Mam nadzieję, że jest to jasne (a przykładów podobnych było duuużo )

Trivial: post'cie? A cóż to za dziwadło.

Jack: nie wiem jak się ten wyraz odmienia...

Eta: jeżeli : post ..... to w poście ( nie należy jeść mięsa)