eh .
KASIA: Proszę o pomoc.
Objętość stożka jest równa 2,25π cm3, a pole jego przekroju osiowego wynosi 4,5cm2.
Oblicz pole powierzchni całkowitej stożka.
będę wdzięczna za wytłumaczenie : )
13 wrz 15:29
think:
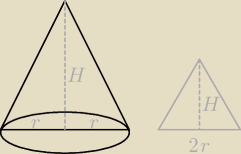
V = πr
2H === 2,25π [cm
3]
| | 1 | |
Pp = |
| *2r*H === 4,5 [cm2] przekrój stożka jest trójkątem równoramiennym zawierającym |
| | 2 | |
średnicę stożka i jego wysokość.
masz do rozwiązania układ równań...
13 wrz 15:43
KASIA: Kurcze sorry, dodałam nie to zadanie ..
To jest poprawne:
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 3 dm.
Oblicz pole powierzchni bocznej o objętość stożka.
13 wrz 15:47
think:
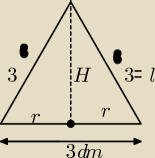
no to przekrój jest taki sam jak w tym wyżej, w podstawie masz średnicę.
2r = 3 [dm] => r = ...
l = 3 [dm]
P
b = π*r*l
13 wrz 15:59
13 wrz 16:08
think: tak
13 wrz 16:11
think: 
a o objętości nie wspominałaś, że w tym zadaniu ma być policzona, ale jest dobrze

13 wrz 16:12
think: ajjj wspominałaś... chyba powinnam iść do okulisty...

13 wrz 16:12
KASIA: ok

dzięki.
a jak wiesz jak zrobić to zadanie ?
Trójkąt prostokątny o przyprostokątnych długości 9 cm i 12 cm obracamy dookoła
przeciwprostokątnej.
Oblicz pole powierzchni całkowitej i objętość otrzymanej bryły.
13 wrz 16:13
think:
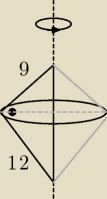
już widzisz co Ci powstanie?
13 wrz 16:33
KASIA: dwa stożki ; ] czyli będzie teraz tak:
P
c=?
V=?
P
c=P
b1+P
b2
V=V
1+V
2
P
c=πR
2+πRl
P
b=πRl
i postawiamy teraz ?
ale ile jest R , bo wiem że jest takie same dla oby dwóch stożków ?
13 wrz 16:41
think: R to jest wysokość opuszczona z wierzchołka C na bok AB
c liczysz z tw pitagorasa
Powodzenia, bo ja na dziś już kończę

13 wrz 16:47
KASIA: ee nie wiem jak ; /
pomocy ..

13 wrz 16:57
think:
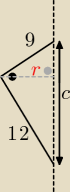
c
2 = 9
2+ 12
2 ⇒ c =...?
| 1 | | 1 | | 9*12 | |
| *9*12 = |
| *c*r ⇒ r = |
| |
| 2 | | 2 | | c | |
13 wrz 22:12
 V = πr2H === 2,25π [cm3]
V = πr2H === 2,25π [cm3]
 no to przekrój jest taki sam jak w tym wyżej, w podstawie masz średnicę.
2r = 3 [dm] => r = ...
l = 3 [dm]
Pb = π*r*l
no to przekrój jest taki sam jak w tym wyżej, w podstawie masz średnicę.
2r = 3 [dm] => r = ...
l = 3 [dm]
Pb = π*r*l
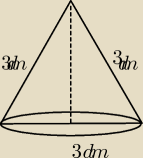 czy to ma być tak ?
http://imageshack.us/photo/my-images/199/obrazvam.jpg/
czy to ma być tak ?
http://imageshack.us/photo/my-images/199/obrazvam.jpg/
 a o objętości nie wspominałaś, że w tym zadaniu ma być policzona, ale jest dobrze
a o objętości nie wspominałaś, że w tym zadaniu ma być policzona, ale jest dobrze

 dzięki.
a jak wiesz jak zrobić to zadanie ?
Trójkąt prostokątny o przyprostokątnych długości 9 cm i 12 cm obracamy dookoła
przeciwprostokątnej.
Oblicz pole powierzchni całkowitej i objętość otrzymanej bryły.
dzięki.
a jak wiesz jak zrobić to zadanie ?
Trójkąt prostokątny o przyprostokątnych długości 9 cm i 12 cm obracamy dookoła
przeciwprostokątnej.
Oblicz pole powierzchni całkowitej i objętość otrzymanej bryły.
 już widzisz co Ci powstanie?
już widzisz co Ci powstanie?


 c2 = 92+ 122 ⇒ c =...?
c2 = 92+ 122 ⇒ c =...?