calka
help: Obliczyc calkę ∬e3x2+3y2dxdy
D: x2+y2≤4
x+y≥0
y≥0
13 wrz 14:22
13 wrz 15:03
Trivial: Z miejsca współrzędne biegunowe. Jakobian r. Potem całka jest banalna.
13 wrz 15:24
Jack:
| | π | |
hm... mi wyszło |
| (e4−1). Pewny jesteś tego wyniku? |
| | 8 | |
13 wrz 15:26
Jack:
ok, zgadza się − nie zmieniłem granic całkowania!
13 wrz 15:28
Trivial:
| | π | |
Mi wychodzi |
| (e12−1). Hm... |
| | 8 | |
13 wrz 15:42
Jack:
Ja tu zrobiłem wcześniej błąd
3r2=t dla 0≤r≤4 czyli t∊<0,16*3>
13 wrz 15:51
Jack:
może o kwadracie przy r zapomniałeś...
13 wrz 15:52
Jack:
dobra... r przecież idzie od 0 do
2.
3r
2=t czyli t∊<0,4*3>
Masz rację
Trivial.

13 wrz 15:58
Trivial:
Ja nie podstawiałem, tylko od razu odgadłem wynik całki
| | 1 | | 1 | |
∫re3r2dr = |
| ∫6re3r2dr = |
| e 3r2 + c.  |
| | 6 | | 6 | |
13 wrz 16:21
help: ehh a mógłby ktoś przedstawic dowolną metode=ę? przyznaje się, że nawet nie chodziłem na ćw i
nie mam zielonego pojcia co to jest jakobian, a tym bardziej jak go wykorzystać...
tak, pójde na koalnach do częstochowy (;
13 wrz 16:28
AC:
Masz rację Trivial

, popełniłem błąd przyjąłem r=4
13 wrz 21:32
Trivial:
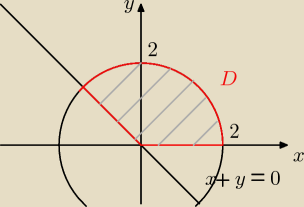
14 wrz 12:29
Trivial:
Tu o zamianie zmiennych:
http://pl.wikipedia.org/wiki/Ca%C5%82ka_podw%C3%B3jna
Od razu 'widać', że jest to całka na współrzędne biegunowe. Jakobian jest r.
Ustalamy granice całkowania.
Trywialne jest, że: 0 ≤ r ≤ 2 (równanie okręgu)
| | 3π | |
Mniej trywialne jest, że: 0 ≤ φ ≤ |
| , ale również można odgadnąć bez liczenia. |
| | 4 | |
| | 3π | |
Czyli nasz obszar całkowania G = [0, 2]x[0, |
| ]. |
| | 4 | |
Jakobian↘ ↙zmienne niezależne.
∬
D e
3x2+3y2dxdy = ∬
G e
3r2*
rdrdφ = ∫
03π/4dφ * ∫
02re
3r2dr =
| | 3π | | 1 | | π | |
= |
| *[ |
| e3r2]02 = |
| (e12 − 1). |
| | 4 | | 6 | | 8 | |
14 wrz 12:38
M.: dziekuje bardzo
a ogolne pytanie dot. calek oznaczonych
skąd wiemy którą funkcję dac do 'wewnatrz' a ktora na zawnatrz;>
14 wrz 18:11
Trivial:
Gdy mamy zmienne niezależne nie ma to znaczenia. Gdy mamy zmienne zależne np. takie:
0 ≤ x ≤ 3
3 + z + x ≤ y ≤ 8 − x
1+x ≤ z ≤ 3x
to idziemy od tych 'najbardziej zależnych', czyli w tym wypadku najpierw y, potem z, potem x.
14 wrz 18:26


 , popełniłem błąd przyjąłem r=4
, popełniłem błąd przyjąłem r=4
