obliczanie pola obszaru ograniczonego krzywymi Paweł: Potrzebuję pomocy w pewnym zadanku. Otóż, jest sobie obszar ograniczony krzywymi:

	1
y=
	x2

y= x y= 3 I teraz, przy obliczaniu pola obszaru za pomocą całki oznaczonej, trzeba określić, która funkcja jest wyższa, a która niższa. No i jak widać, wyższa funkcja jest y=3, a niższa y=x, a

	√3
przedział x−ów jest od		do 3. Jednak nie mogę sobie ot tak walnąć całkę oznaczoną od
	3

	√3		1
		do 3 i ją obliczyć, bo wtedy mi policzy jakby zamiast y=		była prosta y=
	3		x2

	√3
		. Czy można zrobić tak, że po prostu podzielę ten obszar na dwie części, tj. obliczę
	3

	√3
całką pole obszaru z przedziału od		do 1 i dodam pole obszaru z przedziału od 1 do
	3

3? Mam nadzieję, że dobrze wyjaśniłem Liczę na Waszą pomoc.

Bogdan:

	1
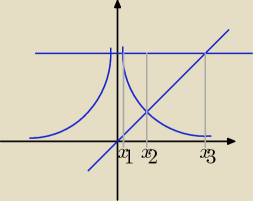
pole P = ∫x1x2 (3 −		)dx + ∫x2x3 (3 − x)dx
	x2

Basia: możesz użyć wartości bezwzględnej i kłopot "z głowy" w tym zadaniu nie ma to specjalnie zastosowania ale np. f(x)=2x² g(x)= x²+1 P = | ₁∫² [f(x)−g(x)]| bez | | musi być g(x)−f(x) bo g(x) "jest wyżej"

Basia: ₋₁∫¹ oczywiście (znaczki mi się poprzestawiały)