Zadania optymalizacyjne cuboy: Z drutu o długości 40cm zbudowano prostokątną ramkę. Znajdz wymiary ramki, która ogranicza największe pole.

Sylwia: 10x10

Sylwia: największe pole, czyli trzeba wykorzystać funkcję kwadratową. robisz układ równań. 2x + 2y = 40 2x = 40 −2y x = 20 − y x = 20 − y f(x) = xy f(x) = xy f(x) = y(20 − y) f(x) = −y² + 20y teraz dla funkcji f(x) = −y² +20y wyznaczasz y_max:

	−20
ymax=		=10
	−2

wyznaczone, czas wrócić do układu równań, a właściwie do jednej jego linijki: x = 20 − y x = 20 − 10 = 10 Odp. Wymiary ramki, która ogranicza największe pole to 10cm x 10cm

Sylwia: tam nie powinno być +20y w pierwszej "części" układu równań. Przeskoczyło mi skądś.

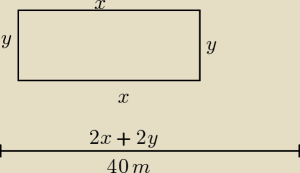
Eta: x,y >0 −−− wymiary ramki 2x+2y=40 to x+y= 20 => y= 20 −x , to x€ (0,20) P= x*y to P(x)= x*(20−x) = −x²+20x −−− to f, kwadratowa, parabola ramionami do dołu zatem osiąga max. dla odciętej wierzchołka

	−20
xw= xmax=		=10 to ymax= 20 −10 =10
	−2

takim prostokątem jest kwadrat o boku dł 10 cm