trójką i środkowa
kamil : W trójkącie ABC w ktorym |AB|=8 i |AC|=12 poprowadzono środkową |CD| i okazało się że
|CD|=|BC|.
Oblicz a) BAC−miara kąta b) długosc srodkowej |CD|
12 wrz 12:40
sushi_ gg6397228:
rysunek zrobiony

12 wrz 13:03
Kamil:
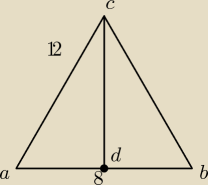
nie wiem tylko czy jest on poprawny.
12 wrz 13:06
sushi_ gg6397228:
na rysunku widac ze CD jest pod katem prostym−−> wiec tak nie moze byc
nie widac aby |BC|= |CD|
12 wrz 13:11
sushi_ gg6397228:
trzeba uzyc dwa razy tw cosinusow
raz do kata ADC
a raz do kata BDC
12 wrz 13:13
kamil:
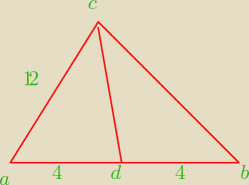
12 wrz 13:14
kamil: i jak uzyc tu tweirdzenia cosinusów ?
12 wrz 13:19
sushi_ gg6397228:
napisalem jakie masz kat−−> patrz na nazwy wierzcholkow−−> od razu widac jai masz wziac trojkat
do reki
12 wrz 13:22
kamil: no tak, ale nie zastosuje tu tw cosinusow skoro nie mam dlugosci c..
12 wrz 13:25
sushi_ gg6397228:
jak zapiszesz dwa rownania, to sie cosinus zredukuje i zostanie jedna zmienna
12 wrz 13:34
kamil: ROZUMIEM, JEDNKA NIE UMIEM ulozyc tych dwóch równań
12 wrz 13:47
sushi_ gg6397228:
zapisz tw cosunusow=== to jest jedno rownanie dla trojkata ADC i kata przy D
niech |CD|=x
12 wrz 13:50
kamil: cos β = 16+x2−1442*4*x
12 wrz 13:56
sushi_ gg6397228:
a Kto kazal przekształcac wzor
a2=b2+c2−2bc cos x zapisujemy w takiej postaci
12 wrz 13:58
kamil: 144=16+x2−8xcosα
12 wrz 13:59
sushi_ gg6397228:
teraz robimy to samo dla trojkata CDB, kat w wierzcholku D
12 wrz 14:02
kamil: x2=16+x2−8xcosα
12 wrz 14:04
sushi_ gg6397228:
a to ciekawe, ze masz taki sam kat−−> na rysunku widac ze jeden z nich jest rozwarty
12 wrz 14:07
kamil: x2=16+x2−8xcosβ
12 wrz 14:08
sushi_ gg6397228:
jezeli tamten kat był "α" to ile stopni moze miec ten kat (uzaleznic od α )
12 wrz 14:11
kamil: x2=16+x2−8xcos(180−α)
12 wrz 14:12
sushi_ gg6397228:
wzory redukcyjne dla cos(180−α)=....
12 wrz 14:13

 nie wiem tylko czy jest on poprawny.
nie wiem tylko czy jest on poprawny.
