Obwód rombu jest równy 20, a suma dlugości jego przekątnych wynosi 12.Oblicz pol arti: Obwód rombu jest równy 20, a suma długości jego przekątnych wynosi 12.Oblicz pole i wysokość tego rombu.

krystek: Znasz obw to znasz bok. A potem policz jego długośc korzystając z tego,że przekątne przecinaja sie pod kątem90 st.

krystek: Miało być'potem dług. przekątnych korzystając z tego,"

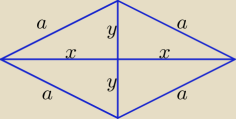
Bogdan: 4a = 20 ⇒ a = 5, x² + y² = 25,

	1
Pole rombu P =		*2x*2y = 2xy
	2

2x + 2y = 12 ⇒ x + y = 6 /² ⇒ x² + 2xy + y² = 36 ⇒ 25 + P = 36 ⇒ P = 11

arti: dzięki

Buzia: dlaczego tam jest x2 + 2xy + y2 = 36 z czego to wynika bo nie moge zrozumieć ?

Eta: x+y=6 /² podniesione obustronnie do kwadratu (x+y)²= 6² ⇒ x²+2xy+y²=36

Buzia: Bo ja w tym zadaniu chciałam zrobić taki układ równań

⎧	x2+y2 = 25
⎩	2x + 2y = 12

	ef
i potem obliczyc Pole rombu ze wzoru na przekątne		no bo e = 2x a f=2y
	2

ale nie wiem czemu wychodzi mi potem dziwna delta i wszystko jest zle

Eta: y= 6−x x²+(6−x)62= 25 2x²−12x+11=0 Licz dalej i będzie ok Δ=56 √Δ= 2√14

	12+2√14		1		1
x=		= 3+		√14 to y= 3−		√14
	4		2		2

2x= 6+√14 i 2y= 6−√14

	(6+√14)(6−√14)		36−14
P=		=		= 11 i jest ten sam wynik
	2		2

ale więcej rachunków niż u Bogdana

Eta: Poprawka zapisu w drugiej linijce : x²+(6−x)²=25

Buzia: Dziekuje ! Zawsze jak mi wychodzi dziwna delta to uważam ze jest wszystko zle

Eta:

Maadzia: Jak obliczyc w tym zadaniu wysokosc rombu ?

Eta: P=a*h ⇒ 5h=11 ⇒ h=...........

hhg: α←∫∊∞Δπγ⇒∑∊≠≈

lukaszp: p⇒a.h⇒5h⇒11⇒5