rysowanie wykresu funkcji kwadratowej ppp44: Narysuj wykres funkcji −x²+4x−3

sushi_ gg6397228: liczysz delte, x₁,x₂, wierzcholek i pare innych punktow i potem sie robi rysunek

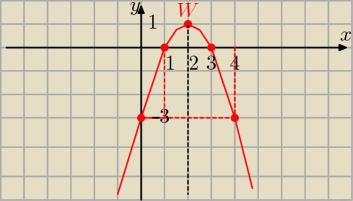
oko: f(x)= −x²+4x −3 f(0)= 3 ( 0,3) f(4)=f(0)=3 f(1)= −1+4 −3=0 (1,0) f(3)= −9+4*3−3=0 (3,0)

	−b
W(xw, yw) xw=		=..... yw=f( xw) =f(2)=.... W(2,1)
	2a

Gustlik: Najlepiej tak: Zrobić obliczenia jak podała oko, a potem przesunąć parabolę y=−x² o wektor w^→=[p, q], gdzie p i q to współrzędne wierzchołka paraboli, zatem przesuwamy o wektor w^→=[2, 1].

Bogdan: p i q to współrzędne wektora przesunięcia paraboli y = −x², ale nie współrzędne wierzchołka paraboli (chodzi o oznaczenia), współrzędne wierzchołka to x_w, y_w. Jeśli przesuwamy parabolę o wierzchołku W₁(0, 0) do W₂(x_w, y_w) o wektor [p, q] to liczbowo x_w = p oraz y_w = q i stąd niesłusznie opisuje się wierzchołek paraboli W(p,q), zamiast W(x_w, y_w). Jeśli przesunięcie paraboli jest o wektor [p, q], ale W₁(x₁≠0, y₁≠0) i W₂(x₂, y₂), to x₂≠p i y₂≠q. Nawet tablice dla maturzystów zawierają tę nieścisłość w oznaczeniach, w tych tablicach wierzchołek paraboli to W(p, q). Wierzcholek to W=(x_w, y_w), wektor przesunięcia w^→=[p, q]. Gustliku i inni udzielający pomocy − mamy obowiązek dbać o poprawność języka matematyki.

Jack: wg mnie nie ma żadnej nieścisłości − równie dobrze we wzorze na postać kanoniczną można rozumieć przez p,q współrzędne wierzchołka, jak i wektor przesunięcia. Niekiedy odczytujemy z "p" i "q" współrzędne wierzchołka, a niekiedy współrzędne wektora przesunięcia − zależnie od potrzeb.