Proszę o sprawdzenie zadania Julia : Punkty A=(1,1), B=(4,3), C=(1,2) i D=(−2,0) tworzą równoległobok. Oblicz jego pole. W odp. mam, że pole wynosi 3, ale mi za każdym razem jak liczę różnymi sposobami wychodzi 2. Mógłby ktoś sprawdzić czy to ja popełniam błąd czy to w odp. jest źle? Proszę

req: sprawdzam

Julia : dziękuję

req: a można wiedzieć jakim spodobem to policzyłas?

Julia : narysowałam na układzie współrzędnych i na jego podstawie obliczałam

req: musisz policzyć jaką długość ma odcinek |AB| i pomnóżyć razy wysokość równoległoboku

Julia : i wtedy wychodzi 3?

req: albo lepiej długości odcinków ^{|DB| * |AC|}₂ i wychodzi 3

req:

3√5
2

Julia : ale w przybliżeniu wyszło mi 3

req: to jest matematyka koleżanko, tu się liczy dokładność

Tad: jednak 3 ...

Julia : no właśnie, ale trochę inaczej policzyłam na współrzędnych i mi wyszło równo 3 dzięki za pomoc

Tad: −odległość punktów A i B (podstawa równoległoboku) wynosi √13 −odległość punktu C od prostej przechodzącej przez punkty A i B

	3
(wysokość równoległoboku) to
	√13

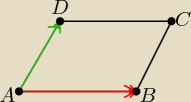
oko: najprościej z wykorzystaniem wektorów → → P=| det(AB, AD) | det −−− wyznacznik pary wektorów zaczepionych w jednym punkcie → → AB=[3,2] AD=[−3,−1] P= | 3*(−1) −(2*(−3)| = | −3+6|= |3|=3 i koniec zadania

oko: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 poczytaj komentarz Gustlika