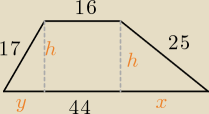
 h = √252 − x2 = √172 − y2
x + y + 16 = 44
625 − x2 = 289 − y2
x = 28 − y
625 − (28−y)2 = 289 − y2
y = 8
h = √289 − 64 = 225
h = 15
h = √252 − x2 = √172 − y2
x + y + 16 = 44
625 − x2 = 289 − y2
x = 28 − y
625 − (28−y)2 = 289 − y2
y = 8
h = √289 − 64 = 225
h = 15
| 44 + 16 | ||
P = | *15 = 450 j2 | |
| 2 |
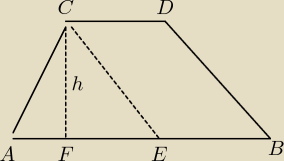 Sposób 2
AB = 44 , CD = 16 , AC = 17 , BD = 25
AE = AB − CD = 44 − 17 = 24 , CE = BD = 25
1. Pole trójkąta ACE obliczyć Heronem
2. Obliczyć wysokość h z pola trójkąta AE*h/2 = S
3. Pole równoległoboku R = BE*h
4. Szukane pole trapezu to suma pól trójkąta i równoległoboku.
Sposób 2
AB = 44 , CD = 16 , AC = 17 , BD = 25
AE = AB − CD = 44 − 17 = 24 , CE = BD = 25
1. Pole trójkąta ACE obliczyć Heronem
2. Obliczyć wysokość h z pola trójkąta AE*h/2 = S
3. Pole równoległoboku R = BE*h
4. Szukane pole trapezu to suma pól trójkąta i równoległoboku.