Rzut prostokątny? Janusz: Pomocy! W równoległoboku ABCD dane są wierzchołki A(1,1), B(5,3) oraz punkt przecięcia przekątnych S(3.4). Oblicz współrzędne punktu E, który jest rzutem prostokątnym punktu B na prostą CD.

Tad: 1) piszesz równanie prostej l przechodzącej przez punkty A i B 2) piszesz równanie prostej m przechodzącej przez punkty A i S 3) wyznaczasz długość odcinka AS i na prostej m znajdujeszwspółrzędne punktu C 4) piszesz równanie prostej n przchodzącej przez punkt C i równoległej do prostej l 5) piszesz równanie prostej p przechodzącej przez punkt B i prostopadłej do prostej n 6) wyznacasz współrżedne punktu E jako punktu przecięcia się prostych p i n

Gustlik: Tad, trochę na okrętkę to robisz. Można tak: Wyznaczam współrzędne punktów C i D:

	1+xC		1+yC
S=(		,		)=(3, 4) jako środek odcinka AC
	2		2

1+xC
	=3 /*2
2

1+x_C=6 x_C=5

1+yC
	=4 /*2
2

1+y_C=8 y_C=7 C=(5, 7)

	5+xD		3+yD
S=(		,		)=(3, 4) jako środek odcinka BD
	2		2

5+xD
	=3 /*2
2

5+x_D=6 x_D=1

3+yD
	=4 /*2
2

3+y_D=8 y_D=5 D=(1, 5) C=(5, 7) D=(1, 5) Wyznaczam prostą CD

	yD−yC		5−7		−2		1
a=		=		=		=
	xD−xC		1−5		−4		2

	1
y=		x+b
	2

wstawiam współrzędne np. D

	1
5=		*1+b
	2

	1
b=4
	2

	1
Pr. CD: y=U{1]{2}x+4
	2

Wyznaczam równanie prostej BE jako prostopadłej do CD: y=−2x+b Wstawiam współrzędne B: 3=−2*5+b 3=−10+b b=13 Pr. BE: y=−2x+13 Współrzędne E znajduję z układu równań prostych CD i BE:

	1		1
y=		x+4
	2		2

y=−2x+13

	1		1
−2x+13=		x+4		/*2
	2		2

−4x+26=x+9 −5x=−17 /:(−5)

	17		2
x=		=3
	5		5

	17
y=−2*		+13 /*5
	5

5y=−34+65 5y=31 /:5

	31		1
y=		=6
	5		5

	2		1
Odp: E=(3		, 6		) − na wszelki wypadek proszę sprawdzic obliczenia, czy nie
	5		5

popełniłem błedu rachunkowego, bo wyszły takie "niezbyt ładne" ułamki.

Tad: bez koment .. bo i po co?

Gustlik: Tad, fakt, to zadanie do najkrótszych nie należy. Sorki, jeżeli Cę uraziłem.

Jack: co za różnica...

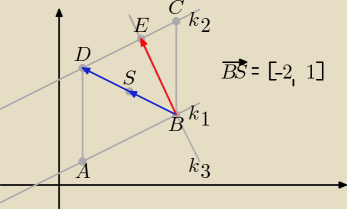
Bogdan: Korzystając ze współrzędnych wektora BS otrzymujemy punkt D A = (1, 1), B = (5, 3), S = (3, 4), D = (−2 + 3, 1 + 4) = (1, 5)

	2
prosta k1: y = a1x + b1, a1 =		= 0,5
	4

prosta k₂: y = a₂x + b₂, k₂ || k₁ ⇒ a₂ = a₁, y = 0,5(x − 1) + 5 ⇒ y = 0,5x + 4,5 prosta k₃: y = a₃x + b₃, k₃⊥k₂ ⇒ a₃ = −2, y = −2(x − 5) + 3 ⇒ y = −2x + 13

⎧	y=0,5x+4,5
⎩	y=−2x+13

x = 3,4 i y=6,2 E = (3,4; 6,2)