stereometria YA: Przekątna ściany sześcianu ma długość 2√3 Oblicz: a) długość przekątnej d sześcianu b) sinus kąta β między krawędzią sześcianu a jego przekątną c) objętość sześcianu Bardzo proszę o wytłumaczenie.

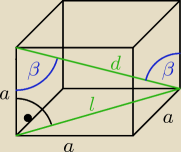
dero2005: a − długość krawędzi sześcianu l − długość przekątnej ściany d − długość przekątnej sześcianu β − kąt pomiędzy krawędzią sześcianu a przekątną sześcianu Ściana sześcianu jest kwadratem o boku a wzór na przekątną kwadratu wynika z twierdzenia Pitagorasa a² + a² = l² gdzie l = 2√3 2a² = l²

	l2
a2 =
	2

	l√2		2√3*√2
a =		=		= √3*√2 = √6 − długość krawędzi
	2		2

długość przekątnej sześcianu d (patrz rys) obliczamy z twierdzenia Pitagorasa a² + l² = d² d = √a² + l² = √(√6)² + (2√3)² = √6 + 12 = √18 = 3√2 − długość przekątnej sześcianu

	l		2√3		√4*√3		12		2
sin β =		=		=		= √		= √
	d		3√2		√9*√2		18		3

Objętość sześcianu V = a³ = (√6)³ = √6*√6*√6 = 6√6

YA: Dziękuję jak nie wiem co jeszcze jedno pytanie: Wzór na długość przekątnej sześcianu, czy to jest wzór na długość odcinka?

dero2005: Wzór na długość przekątnej sześcianu ma postać D = a√3 gdzie a − długość krawędzi sześcianu W przypadku tego zadania przekątna sześcianu została policzona z tw. Pitagorasa "w trójkącie prostokątnym suma kwadratów przyprostokątnych jest równa kwadratowi przeciwprostokątnej" gdzie: krawędź sześcianu − jedna przyprostokątna przekątna ściany − druga przyprostokątna przekątna sześcianu − przeciwprostokątna

krystek: YA →wzór na długość odcinka stosujemy włówczas gdy mamy współrzędne jego końców. Np IAB I gdy A=(x_A;y_A ) B=(x_B;y_B)