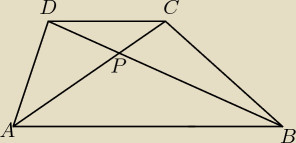
trapez vladimirovna: W trapezie ABCD, AB||CD, niech |AB|= a i |CD|= b. Przekątne tego trapezu przecinają się w p. P. Wówczas: a. |PA|PC|=a:b b. długosc odcinka o końcach należących do ramion trapezu, równoległego do podstaw i przechodzącego przez punkt P, jest rowna 2ab/ (a+b). c. długość odcinka o końcach należących do ramion trapezu, równolrgłego do podstaw i dzielącego

	a2+b2
trapez ABCD na dwa trapezy o równych polach, jest równa √
	2

Wszystkie odp są poprawne

vladimirovna:

vladimirovna: wie ktoś jak to ugryźć? Byłabym serdecznie wdzięczna

oko: http://www.mimuw.edu.pl/delta/artykuly/delta1005/jaszunska.pdf

vladimirovna: o.O dzięki wielkie. Szukaalm w necie coś na temat własnosci w trapezie i nic nei znalazalm. Dziękuję bardzo, na pewno sie przyda

vladimirovna: Mógłby mi ktoś rozjaśnić w średniej harmonicznej drugą linijke obliczeń? Nie wiem skąd się to bierze,

oko: https://matematykaszkolna.pl/forum/37988.html

bereszkakaka: dziękuję oko za pomoc, tutaj jest wszystko pokazane w sposob jasny

vladimirovna: Oko gdybyś mógł mi jeszcze powiedzieć w średniej kwadratowej, ostatnia linijka. Dlaczego licznik został przyrównany do mianownika?

oko:

	L
S=S*		/ :S
	M

L
	=1 => L=M
M

vladimirovna: dzi ekuję

oko: