planimetria
vladimirovna: W kole o długości promienia r poprowadzono dwie przecinające się pod kątem prostym cięciwy AB i
CD. Wyrażenie |AC|2 + |BD|2:
a. ma wartość, ktora zależy od długości cięciw AC i BD
b. jest zawsze równa 2r2
c. jest zawsze równa 4r2
8 wrz 13:59
Tad: c ...

8 wrz 14:25
sushi_ gg6397228:
rysunek zrobiony

8 wrz 14:26
Tad: ... skoro między cięciwami kąt prosty ... to oparty na średnicy ...
8 wrz 14:28
sushi_ gg6397228:
nigdzie nie jest podane ze punkt przeciecia lezy na okregu
8 wrz 14:30
vladimirovna: ale przecież punkt przecięcia się cięciw nie wmusi być na okręgu
zrobiłam rysunek, ale szczerze wątpię by był dobry
8 wrz 14:31
sushi_ gg6397228:
czekamy na niego
8 wrz 14:38
vladimirovna:
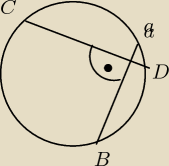
8 wrz 14:46
sushi_ gg6397228:
w odpowiedziach jest : zawsze 4r2 wiec widac ze ta opcja odpada
warto zrobic jeszcze inny rysunek i zmierzyc odcinki AB i CD i sprawdzic(dla siebie) czy
tez bedzie zawsze 2r2
co juz po stwierdzeniu ze nie moze byc zawsze 4r2, tylko w szczegolnym przypadku, odpwoiedz
zawsze 2r2 tez odpada
8 wrz 14:49
vladimirovna: ale poprawna odpowiedź to właśnie C

8 wrz 17:01



