planimetria vladimirovna: Dany jest trójkąt, którego boki mają długość 4,6 i 8. wtedy: a. długość promienia okręgu opisanego na tym trójkącie jest większa od √15 b. dwusieczna największego kąta trójkąta dzieli przeciwległy bok na odcinki, których długości wynoszą 16/5 i 24/5

sushi_ gg6397228:

	abc
policz wzor na pole trojkata (Heron) a potem porownaj z P=
	4R

Eta:

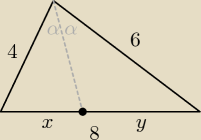
	abc		a+b+c
a) R=		wzór Herona P=√p(p−a)(p−b)(p−c), p=
	4P		2

b) z tw. o dwusiecznej:

4		6
	=		i x+y=8
x		y

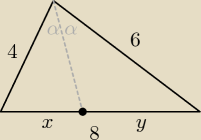
vladimirovna: dziękuję zapomniałam zupełnie tym twierdzeniu