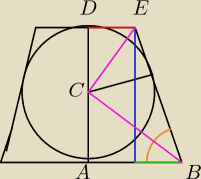Zapisz w prostszej postaci Daria: √11−6√2 √61−28√3

ICSP: pozawijaj to we wzory skróconego mnożenia i skorzystaj z tego że : √a² = |a|

Eta: 1) (3−2√2)²=11−6√2 2) (7−2√3)²= 61−28√3 dalej ,tak jak podał ICSP

ICSP: Jakim cudem tak szybko?

ICSP: Eta mam prośbę

Eta: Ja też

ICSP: to ja już piszę

ICSP: Promień okręgu wpisanego w trapez równoramienny ma długość r. A miara kąta pomiędzy ramieniem trapezu a jego dłuższą postawą wynosi α (alfa). Oblicz pole tego trapezu. Jest to zadanie z tego tematu: https://matematykaszkolna.pl/forum/100800.html Potrafię je rozwiązać sposobem Gustlika ale ja zawsze muszę znaleźć swoją metodę. zielony odcinek oznaczam jako y a czerwony jako x

	2r		2r
tgα =		⇔ y =
	y		tgα

i moja analiza:

	x		r		2r		2r
ΔABC ≈ΔCDE ⇔		=		⇔ r2 = x(x+y) ⇔ r2 = x2 +		x ⇔ x2 +		x −
	r		x+y		tgα		tgα

r² = 0

	4r2
Δ =		+ 4r2
	tg2α

I nie wiem co dalej zrobić.

Eta:

	2r
√Δ=		√1+tg2α
	tgα

ICSP: Boże.

	r
x1 =		(1 + √1 + tg2α)
	tgα

x₂ < 0 − sprzeczne. Dobrze wyznaczyłem?

Eta:

ICSP:

	4x+2y		4r		4r
P =		* 2r = U{4x+2y)r = [		(1 + √1 + tg2α) +		]]r =
	2		tgα		tgα

	4r
[		(2 + √1 + tg2α)]r
	tgα