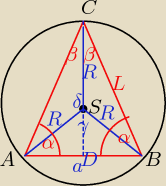
 2β=180−2α
β=90−α
γ=2*2β=360−4α
2β=180−2α
β=90−α
γ=2*2β=360−4α
| 360−γ | ||
δ = | = 2α | |
| 2 |
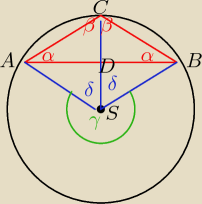 dla α<45 to wygląda tak
β= 90−α
2β= 180−2α
γ= 2*2β = 360−4α
2δ= 4α
δ=2α
2δ=4α
z tr.ASB i tw.cosinusów liczysz AB=2r
z tr.ASC i tw.cosinuów liczysz AC=L
H jak poprzednio
dla α<45 to wygląda tak
β= 90−α
2β= 180−2α
γ= 2*2β = 360−4α
2δ= 4α
δ=2α
2δ=4α
z tr.ASB i tw.cosinusów liczysz AB=2r
z tr.ASC i tw.cosinuów liczysz AC=L
H jak poprzednio
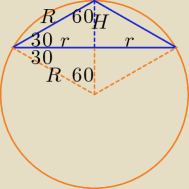 Proponuję takie rozwiązanie:
Wykorzystując warunki zadania otrzymujemy od razu długość tworzącej stożka, jest ona
równa R.
Z własności trójkąta prostokątnego o kątach ostrych 30o i 60o otrzymujemy:
Proponuję takie rozwiązanie:
Wykorzystując warunki zadania otrzymujemy od razu długość tworzącej stożka, jest ona
równa R.
Z własności trójkąta prostokątnego o kątach ostrych 30o i 60o otrzymujemy:
| 1 | 1 | |||
H = | R oraz r = H√3 = | R√3. | ||
| 2 | 2 |
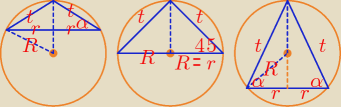 Dane: R, α
t − tworząca stożka, r promień podstawy stożka
Dane: R, α
t − tworząca stożka, r promień podstawy stożka
| t | ||
Z twierdzenia sinusów: | = 2R ⇒ t = 2Rsinα | |
| sinα |
| r | |
= cosα ⇒ r = tcosα = 2Rsinαcosα = Rsin2α | |
| t |