równanie z parametrem Ona.: Całe zadanko zrobiłam oprócz jedego podpunktu, podrzuci ktoś pomysł? Równanie |||x−2|−1|−3| = a, z parametrem a, ma dokładnie 6 rozwiązań dla a należącego: (2,3)? dla okretnej liczby to proste bo podstawimy za a, a jak zrobić coś takiego?

Ona.: ?

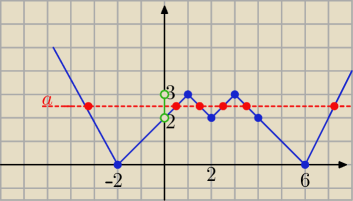
Eta: niebieski wykres (lewej strony ) czerwony ( prawej) dla a€(2,3) obydwa wykresy mają 6 punktów wspólnych

Ona.: proszę pomóżcie

Ona.: dziękuje...

Ona.: tylko jak to zapisać?

Vizer: Rysujesz wykres jak Eta i odczytujesz z wykresu, że tak jest. Ewentualnie można tak zapisać jeszcze: |||x−2|−1|−3| >2 ⋀ |||x−2|−1|−3| <3 i rozwiązać.