KOMBINOWANIE :( MARCIN: w turnieju szachowym rozegrano 66 parti ile było graczy jezeli kazdy z kazdym zagrał jeden raz

Trivial: Wybieramy parę graczy do partii. Nie wiemy ile jest zawodników. Oznaczamy ich ilość przez n.

	n 2
Wybieramy dwóch zawodników z n. Jest dokładnie		możliwości takiego wyboru. Dokładnie

tyle partii rozegrano a więc:

n 2
	= 66.

Obliczyć n.

MARCIN: Dzieki za chec pomocy ale i tak dalej nierozumiem

Trivial: Czego nie rozumiesz?

MARCIN: jak by to powiedziec,jaki jest na to wzor i jak do tego podejsc krok po kroku wiem ze pewnie to głupie ale niemoge nic znalesc a chce w koncu zrozumieć ta matematyke..

Trivial:

	n k
Wzór na takie zadania? Czy wzór na		?

MARCIN: jeżeli mogłbyś tak w skrócie wytłumaczyc to i to?

Trivial:

	n k		n!
Wzór na		=		. Wyprowadzenie tego wzoru jest dosyć skomplikowane, więc w
			k!(n−k)!

tym wypadku lepiej po prostu znać go na pamięć. Opisuje on liczbę wyboru k−elementowych podzbiorów ze zbioru n elementów. Jaśniej, jako że zbiór {a, b} to to samo, co zbiór {b, a} to kolejność wyboru elementów nie ma znaczenia. Przykładowo chcemy wybrać pięcioosobową delegację z grupy 20 osób. Kolejność osób w

	20 5
delegacji nie ma znaczenia − liczy się zbiór wybranych osób. Jest		możliwości

wyboru takiej delegacji. Wzór na takie zadania raczej nie istnieje. Wymagają one myślenia. Na początku należy odpowiedzieć sobie na dwa pytania: 1. Kolejność istotna? (czy rozróżniamy partię gracza 1 z 2 i partię gracza 2 z 1?) − NIE. 2. Elementy mogą się powtarzać? (ta sama osoba nie może grać z tą samą osobą) − NIE. Pomogą one przynajmniej wybrać odpowiedni wzór. Jeżeli dalej nie rozumiesz czegoś to pytaj.

MARCIN: a w tym moim zadaniu na miejscu K co to jest to 2?

Trivial: Tak.

Trivial: Wybieramy dwóch graczy ze zbioru wszystkich graczy. Nie wiemy jeszcze ile jest wszystkich graczy, więc oznaczamy n − ilość graczy.

n 2
	.

Rozegrano 66 partii, przy czym każdy zagrał z każdym, a więc:

n 2
	= 66.

Rozpisujemy n!↘

n 2		n!		(n−2)!*(n−1)n		n(n−1)
	=		=		=		= 66.
		2!(n−2)!		2*(n−2)!		2

MARCIN: ale co to własnie jest to 2?

Trivial: Wybieramy parę graczy, którzy rozegrają partię. Para, czyli 2.

MARCIN: dobra szkoda może twojego czasu,ale nieumiem wogule tego zostosować do tego zadania tak do konca

MARCIN: w ogóle*

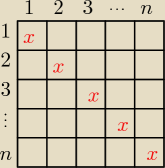
Trivial: Można też narysować całą sytuację, ale to wymaga więcej czasu. Tabelka: x − gracze nie grają sami ze sobą. Wszystkich pól w kwadracie jest n². Pól na przekątnej jest n. n²−n Partia np. (2,3) to to samo co partia (3,2). Każda partia była liczona dwa razy, a więc ostatecznie mamy:

n2−n		n(n−1)
	=		= 66.
2		2

Trivial: To naprawdę nie jest takie trudne, wystarczy poćwiczyć.

MARCIN: ok ale kiedy wyjdzie wynik

Trivial: Trzeba rozwiązać równanie:

n(n−1)
	= 66.
2

czyli: n² − n = 132 n² − n − 132 = 0 Δ = ... n₁, n₂ = ... Potem odrzucamy rozwiązanie, gdy n nie jest liczbą naturalną i mamy wynik.